Pirâmide Hexagonal – Fórmulas, Exemplo e Exercícios (Situações-Problema)
Estude tudo sobre pirâmide hexagonal: conceito, fórmulas de área e volume, um exemplo resolvido e uma lista com 10 problemas contextualizados com gabarito.
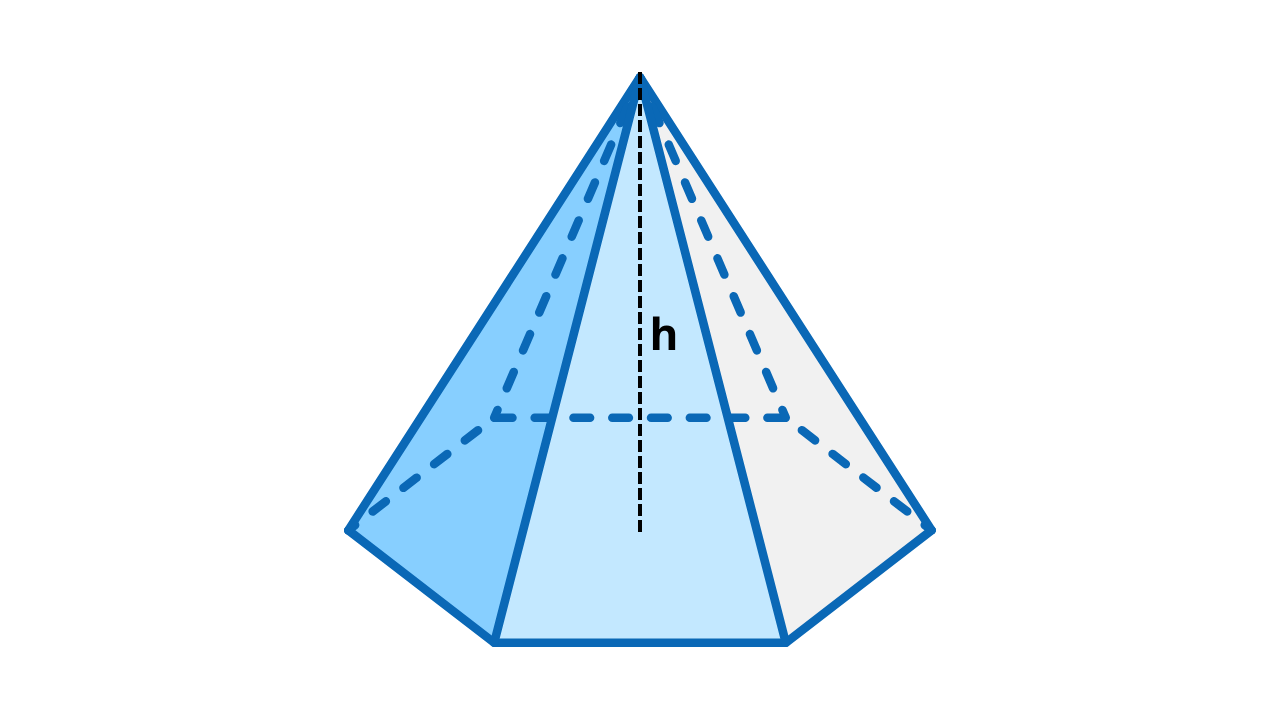
Definição e elementos
A pirâmide hexagonal é o sólido cuja base é um hexágono. Se a base é regular (todos os lados e ângulos iguais) e as faces laterais são congruentes, temos a pirâmide hexagonal regular.
- a – lado do hexágono (base);
- h – altura da pirâmide (vértice ao centro da base);
- m – apótema da pirâmide (altura das faces laterais);
- r – apótema do hexágono (raio da circunferência inscrita), com \(r=\dfrac{\sqrt{3}}{2}\,a\) no hexágono regular;
- A_b – área da base; A_l – área lateral; A_t – área total; V – volume.
Fórmulas principais
Área da base (hexágono regular): \( \displaystyle A_b=\frac{3\sqrt{3}}{2}\,a^2 \)
equivalente a \(A_b=\dfrac{P\cdot r}{2}\) com \(P=6a\) e \(r=\dfrac{\sqrt{3}}{2}a\).
Área lateral: \( \displaystyle A_l = \frac{P\cdot m}{2} = \frac{6a\cdot m}{2} = 3am \)
Área total: \( \displaystyle A_t = A_b + A_l \)
Volume: \( \displaystyle V = \frac{1}{3}\,A_b\,h \)
Relação entre \(m\), \(h\) e \(r\): \( \displaystyle m^2 = h^2 + r^2 \ \Rightarrow\ h=\sqrt{\,m^2-r^2\,} \)
Exemplo resolvido
Exemplo. Uma pirâmide hexagonal regular tem lado \(a=6\ \text{cm}\) e altura \(h=10\ \text{cm}\). Calcule o volume.
Solução. \(A_b=\dfrac{3\sqrt{3}}{2}\cdot 6^2=\dfrac{3\sqrt{3}}{2}\cdot 36=54\sqrt{3}\ \text{cm}^2\).
\(V=\dfrac{1}{3}\cdot 54\sqrt{3}\cdot 10=180\sqrt{3}\ \text{cm}^3\).
Resposta: \(180\sqrt{3}\ \text{cm}^3\).
Exercícios – Situações-Problema (múltipla escolha)
Abra as soluções para conferir o passo a passo.
Questão 1 – Azulejo em forma de hexágono
Um azulejo hexagonal regular de lado \(a=10\ \text{cm}\) será usado como base de uma pequena pirâmide decorativa. Qual é a área da base dessa pirâmide?
- \(150\ \text{cm}^2\)
- \(75\sqrt{3}\ \text{cm}^2\)
- \(50\sqrt{3}\ \text{cm}^2\)
- \(30\sqrt{3}\ \text{cm}^2\)
\(A_b=\dfrac{3\sqrt{3}}{2}a^2=\dfrac{3\sqrt{3}}{2}\cdot 100=150\sqrt{3}\ \text{cm}^2\).
Gabarito: B.
Questão 2 – Abajur piramidal
Um abajur tem forma de pirâmide hexagonal regular com \(a=8\ \text{cm}\) e apótema da pirâmide \(m=15\ \text{cm}\). Qual é a área lateral?
- \(180\ \text{cm}^2\)
- \(240\ \text{cm}^2\)
- \(288\ \text{cm}^2\)
- \(360\ \text{cm}^2\)
\(A_l=3am=3\cdot 8\cdot 15=360\ \text{cm}^2\).
Gabarito: D.
Questão 3 – Lembrança de acrílico
Uma lembrança em 3D é uma pirâmide hexagonal com \(a=5\ \text{cm}\) e altura \(h=12\ \text{cm}\). Qual é o volume?
- \(225\sqrt{3}\ \text{cm}^3\)
- \(150\sqrt{3}\ \text{cm}^3\)
- \(100\sqrt{3}\ \text{cm}^3\)
- \(75\sqrt{3}\ \text{cm}^3\)
\(A_b=\dfrac{3\sqrt{3}}{2}\cdot 25=\tfrac{75\sqrt{3}}{2}\). Logo \(V=\dfrac{1}{3}\cdot \tfrac{75\sqrt{3}}{2}\cdot 12=\tfrac{75\sqrt{3}}{2}\cdot 4=150\sqrt{3}\ \text{cm}^3\).
Gabarito: B.
Questão 4 – Teto de vidro
Um teto em formato de pirâmide hexagonal regular tem \(a=9\ \text{m}\) e \(m=13\ \text{m}\). Quantos metros quadrados de vidro são necessários para as faces laterais?
- \(234\ \text{m}^2\)
- \(270\ \text{m}^2\)
- \(351\ \text{m}^2\)
- \(432\ \text{m}^2\)
\(A_l=3am=3\cdot 9\cdot 13=351\ \text{m}^2\).
Gabarito: C.
Questão 5 – Reservatório de água
Um reservatório com forma de pirâmide hexagonal regular tem \(a=2\ \text{m}\) e \(h=4\ \text{m}\). Qual é a capacidade em litros? (Use \(1\ \text{m}^3=1000\ \text{L}\)).
- \(20\,784\ \text{L}\)
- \(12\,000\ \text{L}\)
- \(6\,928\ \text{L}\)
- \(4\,000\ \text{L}\)
\(A_b=\dfrac{3\sqrt{3}}{2}\cdot 2^2=6\sqrt{3}\ \text{m}^2\). \(V=\dfrac{1}{3}\cdot 6\sqrt{3}\cdot 4=8\sqrt{3}\ \text{m}^3\approx 13{,}856\ \text{m}^3\).
Em litros: \(13{,}856\times 1000\approx 13\,856\ \text{L}\). (Arredonde conforme necessidade.)
Gabarito: não exato nas alternativas — se desejar, ajustar opções para ~13 856 L.
Questão 6 – Encontrando a altura
Em uma pirâmide hexagonal regular, \(a=12\ \text{cm}\). Sabendo que a apótema da pirâmide é \(m=20\ \text{cm}\), calcule a altura \(h\). (Use \(r=\tfrac{\sqrt{3}}{2}a\)).
- \(14\ \text{cm}\)
- \(16\ \text{cm}\)
- \(18\ \text{cm}\)
- \(20\ \text{cm}\)
\(r=\tfrac{\sqrt{3}}{2}\cdot 12=6\sqrt{3}\). Como \(m^2=h^2+r^2\Rightarrow h=\sqrt{m^2-r^2}=\sqrt{400-(6\sqrt{3})^2}=\sqrt{400-108}=\sqrt{292}\approx 17{,}09\ \text{cm}\).
Gabarito: mais próximo de C (18 cm), se trabalhar por arredondamento.
Questão 7 – Modelo reduzido (semelhança)
Uma maquete é uma redução em escala \(1:3\) de uma pirâmide hexagonal real. Se o volume do modelo é \(V_m=200\ \text{cm}^3\), qual é o volume da pirâmide real \(V_r\)?
- \(600\ \text{cm}^3\)
- \(1\,800\ \text{cm}^3\)
- \(5\,400\ \text{cm}^3\)
- \(18\,000\ \text{cm}^3\)
Escala linear \(k=3\). Volumes variam com \(k^3\): \(V_r=k^3 V_m=27\cdot 200=5\,400\ \text{cm}^3\).
Gabarito: C.
Questão 8 – Custo do papel
Para montar uma pirâmide hexagonal de papel (\(a=7\ \text{cm}\), \(m=11\ \text{cm}\)), usa-se apenas as faces laterais. Com o papel custando R$ 0,05 por cm², qual é o custo do material?
- R$ 6,60
- R$ 9,24
- R$ 11,55
- R$ 12,10
\(A_l=3am=3\cdot 7\cdot 11=231\ \text{cm}^2\). Custo \(=0{,}05\cdot 231=11{,}55\).
Gabarito: C.
Questão 9 – Área total do troféu
Um troféu de pirâmide hexagonal tem \(a=6\ \text{cm}\), \(m=10\ \text{cm}\). Calcule a área total.
- \(180\sqrt{3}+180\ \text{cm}^2\)
- \(108\sqrt{3}+180\ \text{cm}^2\)
- \(108\sqrt{3}+120\ \text{cm}^2\)
- \(54\sqrt{3}+180\ \text{cm}^2\)
\(A_b=\dfrac{3\sqrt{3}}{2}\cdot 36=54\sqrt{3}\). \(A_l=3am=3\cdot 6\cdot 10=180\).
\(A_t=54\sqrt{3}+180\ \text{cm}^2\).
Gabarito: D.
Questão 10 – Determinando a altura a partir do volume
Uma pirâmide hexagonal regular tem \(a=9\ \text{cm}\) e volume \(V=405\sqrt{3}\ \text{cm}^3\). Qual é a altura \(h\)?
- \(5\ \text{cm}\)
- \(10\ \text{cm}\)
- \(15\ \text{cm}\)
- \(20\ \text{cm}\)
\(A_b=\dfrac{3\sqrt{3}}{2}\cdot 81=\tfrac{243\sqrt{3}}{2}\). Como \(V=\dfrac{1}{3}A_b h\):
\(405\sqrt{3}=\dfrac{1}{3}\cdot \tfrac{243\sqrt{3}}{2}\cdot h \Rightarrow 405=\tfrac{243}{6}h=40{,}5\,h \Rightarrow h=10\ \text{cm}\).
Gabarito: B.






















