Pirâmide Triangular: Definição, Fórmulas e Exercícios Resolvidos
Aprenda tudo sobre a pirâmide triangular: elementos, área, volume, exemplos resolvidos e lista de exercícios. Geometria Espacial para ENEM e concursos.
O que é uma Pirâmide Triangular?
A pirâmide triangular é um sólido geométrico cuja base é um triângulo. Suas demais faces também são triângulos, totalizando quatro faces. Esse tipo de pirâmide é muito comum em problemas de pirâmides na Geometria Espacial.
Quando todas as arestas são iguais, temos uma pirâmide regular, chamada também de tetraedro regular.
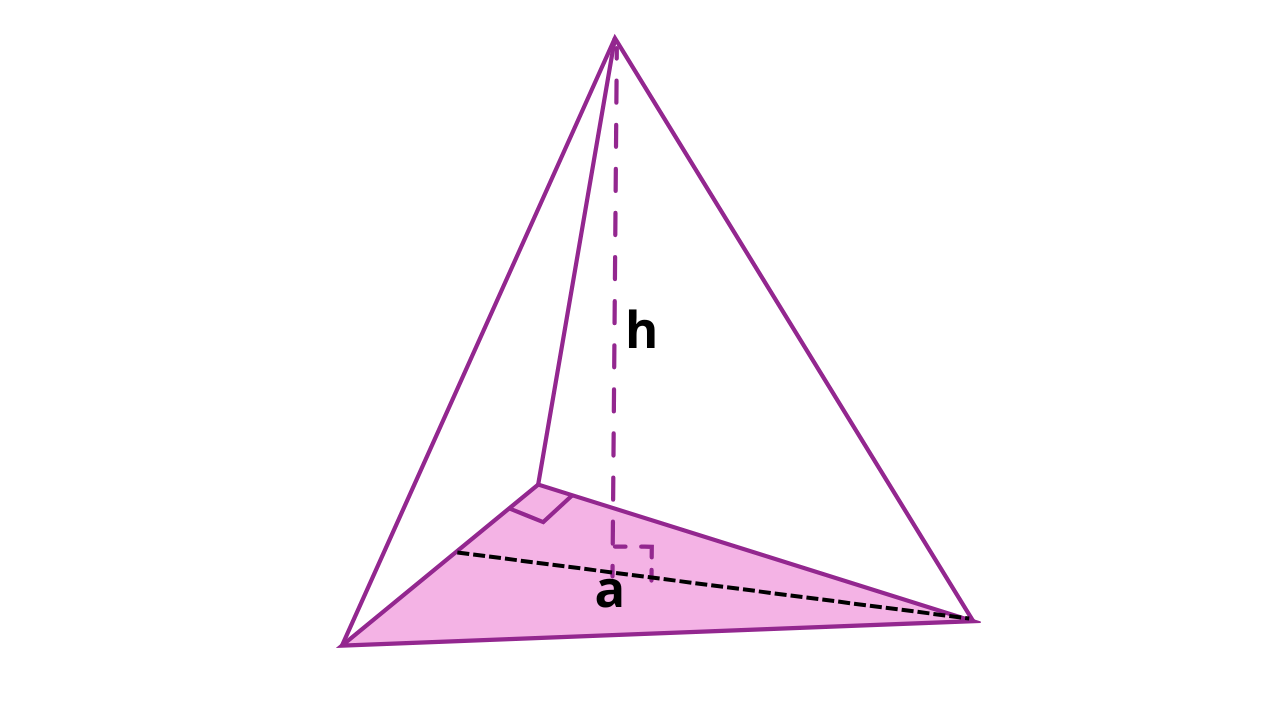
Elementos da Pirâmide Triangular
- a: lado da base (triângulo);
- h: altura da pirâmide (do vértice ao plano da base);
- Faces: 4 triângulos (sendo 1 a base e 3 laterais);
- Arestas: 6;
- Vértices: 4.
Fórmulas da Pirâmide Triangular
Área da base (triângulo equilátero):
\( A_b = \dfrac{a^2\sqrt{3}}{4} \)
Volume:
\( V = \dfrac{1}{3}\cdot A_b \cdot h \)
Área total:
\( A_T = A_b + A_{faces\ laterais} \)
Exemplo Resolvido
Calcule o volume de uma pirâmide triangular regular com lado da base \(a=6\ \text{cm}\) e altura \(h=9\ \text{cm}\).
Área da base: \(A_b=\tfrac{a^2\sqrt{3}}{4}=\tfrac{36\sqrt{3}}{4}=9\sqrt{3}\ \text{cm}^2\).
Volume: \(V=\tfrac{1}{3}\cdot 9\sqrt{3}\cdot 9=27\sqrt{3}\ \text{cm}^3\).
Resposta: \(27\sqrt{3}\ \text{cm}^3\).
Exercícios de Fixação
Questão 1
Uma pirâmide triangular tem lado da base \(a=4\ \text{cm}\). Qual é a área da base?
- 2√3 cm²
- 4√3 cm²
- 6√3 cm²
- 8√3 cm²
\(A_b=\tfrac{a^2\sqrt{3}}{4}=\tfrac{16\sqrt{3}}{4}=4\sqrt{3}\ \text{cm}^2\).
Resposta correta: B
Questão 2
Calcule o volume de uma pirâmide triangular com base \(a=6\ \text{cm}\) e altura \(h=10\ \text{cm}\).
- 15√3 cm³
- 25√3 cm³
- 30√3 cm³
- 50√3 cm³
\(A_b=\tfrac{a^2\sqrt{3}}{4}=\tfrac{36\sqrt{3}}{4}=9\sqrt{3}\).
\(V=\tfrac{1}{3}\cdot 9\sqrt{3}\cdot 10=30\sqrt{3}\ \text{cm}^3\).
Resposta correta: C
🔗 Continue estudando Geometria Espacial
📚 Materiais do Matemática Hoje
Acelere sua preparação com nossos conteúdos premium:






















