Planificação do Prisma Pentagonal
Veja como montar a planificação (net), quais fórmulas usar e resolva exemplos práticos com cálculo de área da chapa.
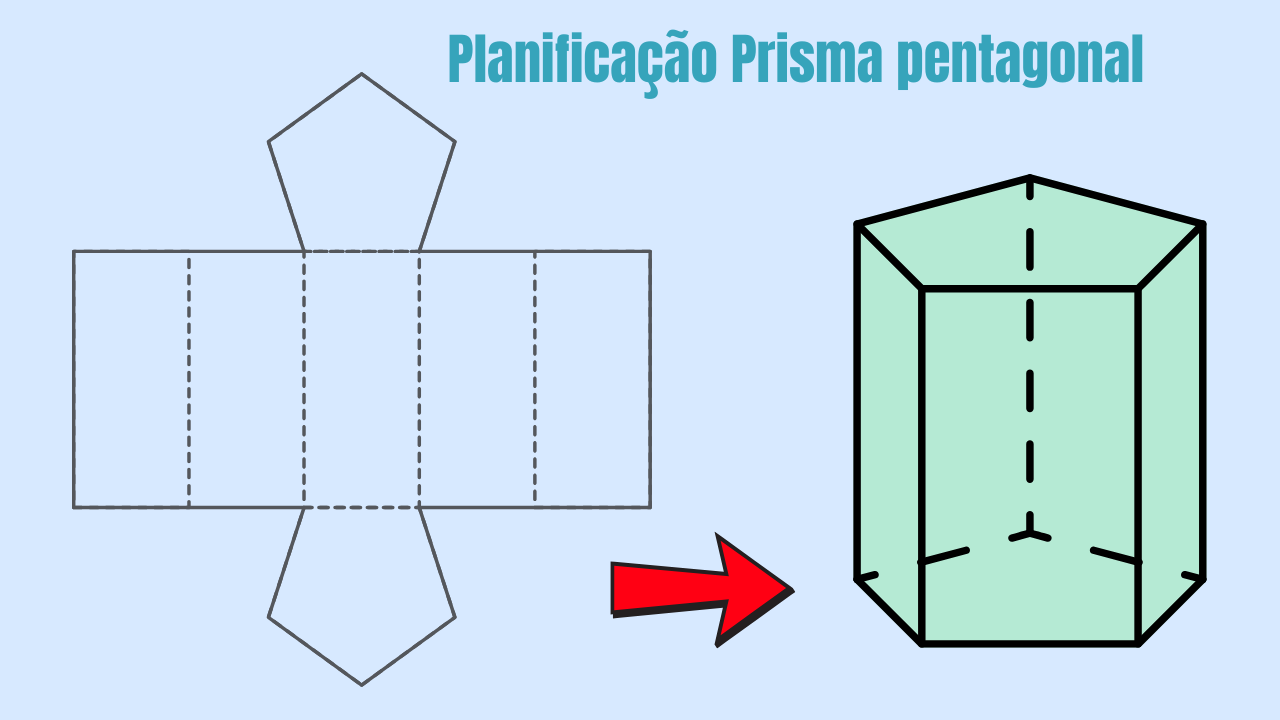
1) O que é a planificação de um prisma pentagonal?
É o desenho plano obtido ao “abrir” o prisma. Para o prisma pentagonal reto, a planificação tem:
- Faixa lateral: um retângulo de dimensões \(p\times h\), em que \(p\) é o perímetro do pentágono da base e \(h\) é a altura do prisma;
- 5 retângulos na faixa, com larguras iguais aos lados do pentágono e altura \(h\);
- 2 pentágonos congruentes (as bases).
Para relembrar a ideia em outros sólidos, veja: Planificação do Cubo e Planificação do Paralelepípedo.
2) Como montar a planificação (passo a passo)
- Desenhe um retângulo \(p\times h\) (faixa lateral) e marque nele os cinco segmentos de largura iguais aos lados do pentágono: \(a_1,a_2,a_3,a_4,a_5\) (a soma é \(p\)).
- Acople um pentágono em uma das bordas maiores; acople o outro pentágono na borda oposta (ou próximo ao último retângulo).
- Se for um molde de papel, adicione abas de cola (por exemplo, 1 cm) ao longo de uma aresta lateral e no entorno de uma base.
- Recorte, dobre nas linhas pontilhadas e una pelas abas.
3) Fórmulas úteis na planificação
Para base pentagonal regular de lado \(a\) e apótema \(r\):
Sem apótema: \(A_b=\dfrac{a^2}{4}\sqrt{25+10\sqrt5}\).
4) Exemplos resolvidos (situação + solução em abre/fecha)
Exemplo 1 — Molde escolar (prisma pentagonal regular)
Situação-problema. Você vai imprimir um molde de prisma pentagonal regular em cartolina. O lado do pentágono é \(a=9\ \text{cm}\) e a altura do prisma é \(h=14\ \text{cm}\). Calcule a área da chapa sem abas (planificação completa: faixa lateral + duas bases).
Ver solução
Aproximação: \(\sqrt{25+10\sqrt5}\approx 6{,}8820\) → \(A_b\approx 139{,}39\), \(A_{\text{chapa}}\approx 630 + 278{,}98 = 908{,}98\ \text{cm}^2\).
Exemplo 2 — Planificação com aba de cola
Situação-problema. No Exemplo 1, adicione uma aba de cola de 1 cm de largura ao longo de uma única aresta lateral (altura \(h=14\ \text{cm}\)). Qual a área extra e qual fica a nova área da chapa?
Ver solução
Aproximação: \(908{,}98 + 14 = 922{,}98\ \text{cm}^2\).
Exemplo 3 — Base qualquer e perímetro conhecido
Situação-problema. Um prisma pentagonal (não necessariamente regular) tem perímetro da base \(p=52\ \text{cm}\), área de uma base \(A_b=160\ \text{cm}^2\) e altura \(h=18\ \text{cm}\). Calcule a área da faixa lateral e a área da chapa (sem abas).
Ver solução
5) Exercícios propostos
- (Regular) \(a=7\ \text{cm}\), \(h=20\ \text{cm}\). Calcule \(A_L\) e a área da chapa (sem abas).
- (Regular) \(a=10\ \text{cm}\), apótema \(r=6{,}9\ \text{cm}\), \(h=25\ \text{cm}\). Calcule \(A_b\), \(A_{\text{chapa}}\).
- (Geral) \(p=48\ \text{cm}\), \(A_b=150\ \text{cm}^2\), \(h=12\ \text{cm}\). Ache \(A_L\) e \(A_{\text{chapa}}\).
- (Aba) No item 1, inclua aba lateral de \(1{,}5\ \text{cm}\) e abas de \(0{,}8\ \text{cm}\) em toda a borda de uma base. Qual a nova área?
- (Corte) Uma folha \(30\times 40\ \text{cm}\) precisa comportar a planificação de um prisma pentagonal regular com \(a=6\ \text{cm}\), \(h=18\ \text{cm}\) (sem abas). É possível? Justifique pela área e por uma organização plausível das peças.






















