Plano Cartesiano
Eixos, quadrantes, localização de pontos, distância, ponto médio, inclinação e equação da reta.
O plano cartesiano é formado pelos eixos perpendiculares x (horizontal) e y (vertical). Eles se cruzam na origem \(O=(0,0)\). Um ponto \(P\) é um par ordenado \(P(x,y)\). Para revisar conteúdos ligados, veja Conjuntos Numéricos, Mapas Mentais e o Banco de Questões.
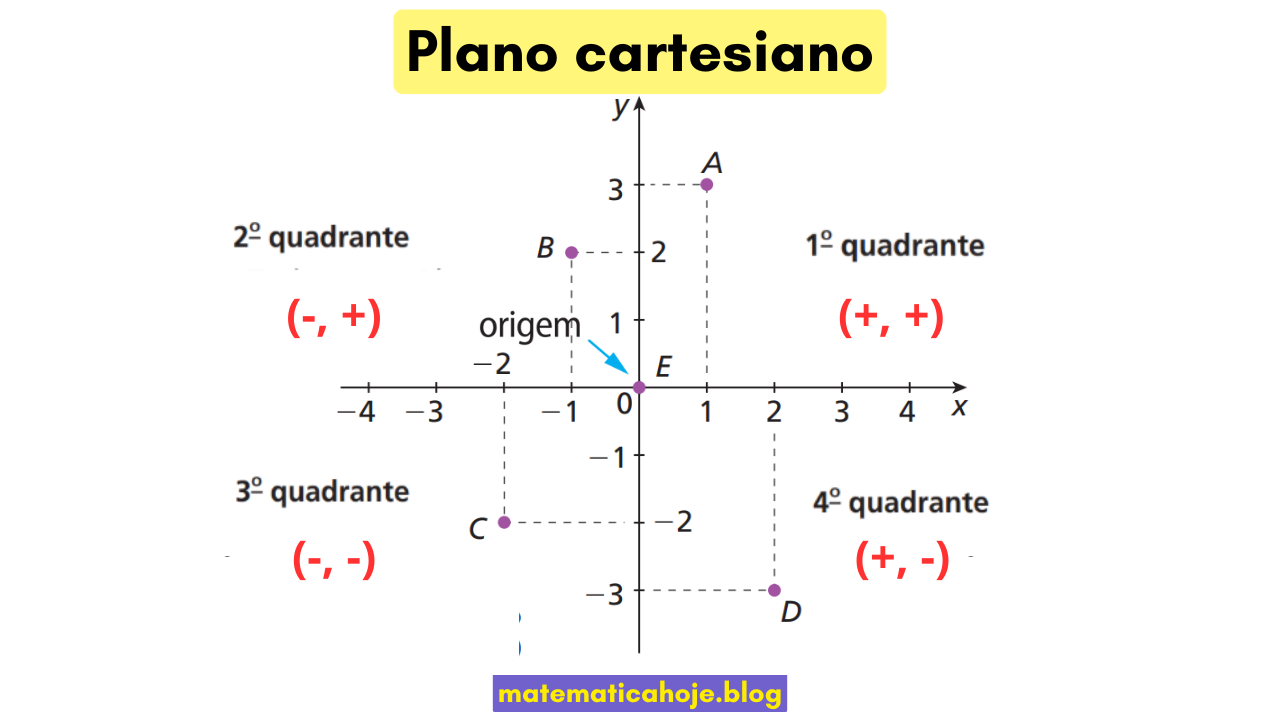
Quadrantes e sinais
| Quadrante | Sinais | Exemplo |
|---|---|---|
| 1º | \((+,+)\) | \((2,3)\) |
| 2º | \((-,+)\) | \((-1,2)\) |
| 3º | \((-,-)\) | \((-2,-1)\) |
| 4º | \((+,-)\) | \((3,-2)\) |
No desenho: \(A=(1,3)\), \(B=(-1,2)\), \(C=(-2,-2)\), \(D=(2,-3)\) e \(E=(0,0)\).
Fórmulas essenciais
- Distância \(d\) entre \(P_1(x_1,y_1)\) e \(P_2(x_2,y_2)\): \(d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}\)
- Ponto médio de \(A(x_1,y_1)\) e \(B(x_2,y_2)\): \(M\!\left(\dfrac{x_1+x_2}{2},\,\dfrac{y_1+y_2}{2}\right)\)
- Inclinação (coeficiente angular) por \(P_1,P_2\): \(m=\dfrac{y_2-y_1}{x_2-x_1}\) (\(x_2\neq x_1\))
- Equação da reta com inclinação \(m\) e intercepto \(b\): \(y=mx+b\)
Exemplos
1) Em qual quadrante está \((-4,2)\)?
Sinais \((-,+)\) ⇒ 2º quadrante.
2) Distância entre \(A(1,3)\) e \(B(-1,2)\)
\(d=\sqrt{(1-(-1))^2+(3-2)^2}=\sqrt{2^2+1^2}=\sqrt{5}\).
3) Ponto médio de \(C(-2,-2)\) e \(D(2,-3)\)
\(M=\left(\dfrac{-2+2}{2},\dfrac{-2-3}{2}\right)=(0,-\tfrac{5}{2})\).
4) Reta que passa por \(E(0,0)\) e \(A(1,3)\)
Inclinação \(m=\dfrac{3-0}{1-0}=3\). Como passa pela origem, \(b=0\). Logo, \(y=3x\).
Exercícios (múltipla escolha) com solução
1) O ponto \(P(-3,-1)\) pertence a qual quadrante?
- 1º
- 2º
- 3º
- 4º
Ver solução
2) A distância entre \(A(2,5)\) e \(B(-1,1)\) é:
- 3
- 4
- 5
- 6
Ver solução
3) O ponto médio do segmento que une \(A(-4,2)\) e \(B(6,0)\) é:
- \((1,1)\)
- \((0,1)\)
- \((2,1)\)
- \((1,0)\)
Ver solução
4) A inclinação da reta que passa por \(P(1,2)\) e \(Q(4,8)\) é:
- 2
- \(\tfrac{2}{3}\)
- 3
- \(\tfrac{8}{4}\)
Ver solução
5) A reta que passa por \(R(2,3)\) com inclinação \(m=-\tfrac12\) tem equação:
- \(y=-\tfrac12x+4\)
- \(y=-\tfrac12x+2\)
- \(y=\tfrac12x+3\)
- \(y=-2x+3\)
Ver solução
6) Se a reta tem intercepto \(b=-3\) e inclinação \(m=3\), sua equação é:
- \(y=3x-3\)
- \(y=3x+3\)
- \(y=-3x+3\)
- \(y=-3x-3\)






















