Poliedros e Corpos Redondos — conceitos, fórmulas, exemplos e exercícios
Este guia visual foi inspirado na imagem abaixo e organiza, de forma simples, os sólidos mais presentes nos vestibulares, ENEM e concursos: poliedros (cubo, prismas, paralelepípedo e pirâmides) e corpos redondos (cilindros, cones e esferas). Você verá fórmulas essenciais, exemplos resolvidos linha a linha e exercícios com gabarito em sistema abre/fecha.
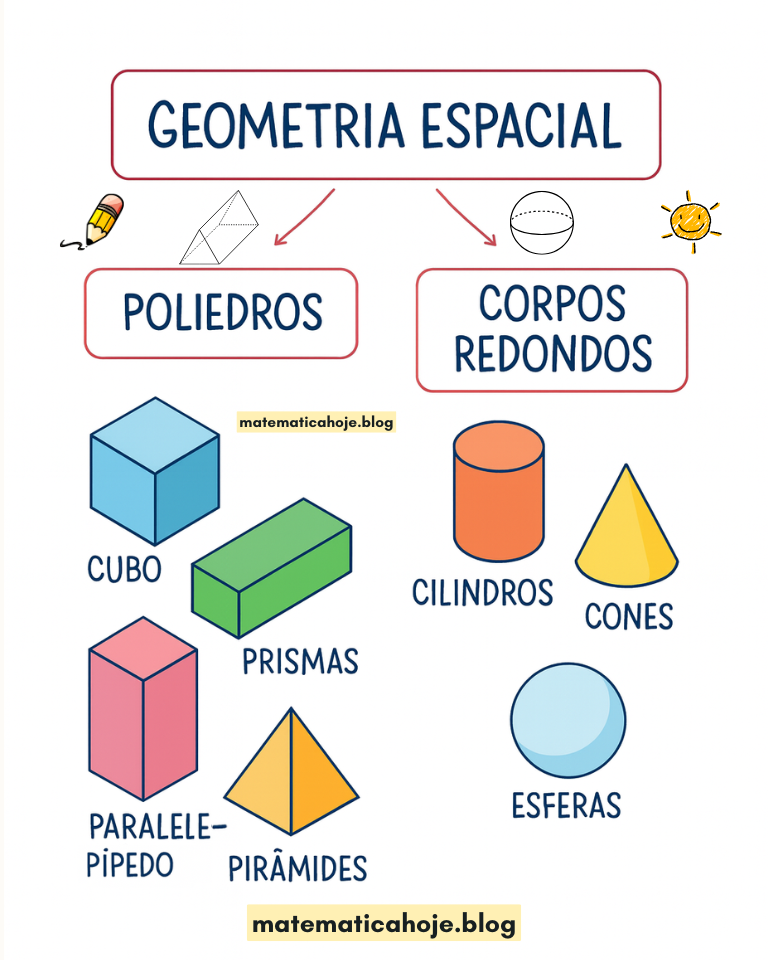
1) O que são poliedros?
Poliedros são sólidos formados apenas por faces planas (polígonos). Têm arestas (encontros entre faces) e vértices (encontros entre arestas).
Cubo
Se a aresta mede \(a\):
Volume: \(V = a^3\)
Paralelepípedo retângulo
Com dimensões \(a, b, c\):
Volume: \(V = abc\)
Prisma reto
Base de área \(A_b\) e altura \(h\):
Pirâmide
Base de área \(A_b\) e altura \(h\):
Exemplo 1 — volume do cubo
Enunciado. Um cubo tem aresta \(a=3\) cm. Calcule o volume.
V = \(a^3\) = \(3^3\) = \(27\ \text{cm}^3\)
Exemplo 2 — área do paralelepípedo
Enunciado. Um paralelepípedo tem \(a=2\) cm, \(b=4\) cm e \(c=5\) cm. Encontre a área total.
A_T = \(2(ab+ac+bc)\) = \(2(2\cdot4 + 2\cdot5 + 4\cdot5)\) = \(2(8 + 10 + 20)\) = \(2\cdot38\) = \(76\ \text{cm}^2\)
2) O que são corpos redondos?
Corpos redondos possuem pelo menos uma superfície curva. Os principais são o cilindro, o cone e a esfera.
Cilindro
Raio \(r\) e altura \(h\):
Área total: \(A_T = 2\pi r(h + r)\)
Volume: \(V = \pi r^2 h\)
Cone reto
Raio \(r\), altura \(h\) e geratriz \(g\) (\(g^2=r^2+h^2\)):
Área total: \(A_T = \pi r(g + r)\)
Volume: \(V = \dfrac{\pi r^2 h}{3}\)
Esfera
Volume: \(V = \dfrac{4}{3}\pi r^3\)
Exemplo 3 — volume do cilindro
Enunciado. Uma lata tem raio \(r=4\) cm e altura \(h=12\) cm. Determine o volume.
V = \(\pi r^2 h\) = \(\pi\cdot4^2\cdot12\) = \(\pi\cdot16\cdot12\) = \(192\pi\ \text{cm}^3\)
Exemplo 4 — área da esfera
Enunciado. Calcule a área de uma esfera de raio \(r=5\) cm.
A = \(4\pi r^2\) = \(4\pi\cdot5^2\) = \(4\pi\cdot25\) = \(100\pi\ \text{cm}^2\)
Materiais que aceleram seus estudos
Organize o conteúdo com nossos materiais exclusivos:
- 📌 Mapas Mentais de Matemática (coleção completa — destaque).
- 📚 ENEM Matemática — trilha de revisão focada.
- 📕 10 eBooks de Matemática — pacote econômico.
- 🧩 Banco de Questões — centenas de itens com solução.
- 📥 eBook Gratuito de Fórmulas (baixe agora — destaque).
3) Exercícios (com soluções em abre/fecha)
Q1 — (Múltipla escolha) Um cubo tem volume \(216\ \text{cm}^3\). O valor da aresta é:
Alternativas: A) 5 cm B) 6 cm C) 8 cm D) 9 cm
Solução. \(V=a^3\) = \(216\) \(\Rightarrow a=\sqrt[3]{216}\) = \(6\ \text{cm}\)
Gabarito: B
Q2 — (Discursiva) Um prisma de base triangular tem \(A_b=30\ \text{cm}^2\) e altura \(h=10\ \text{cm}\). Calcule o volume.
V = \(A_b\cdot h\) = \(30\cdot10\) = \(300\ \text{cm}^3\)
Q3 — (Múltipla escolha) Um paralelepípedo tem dimensões \(2\ \text{cm}\), \(3\ \text{cm}\) e \(7\ \text{cm}\). A área total é:
Alternativas: A) \(64\ \text{cm}^2\) B) \(82\ \text{cm}^2\) C) \(94\ \text{cm}^2\) D) \(106\ \text{cm}^2\)
A_T = \(2(ab+ac+bc)\) = \(2(2\cdot3 + 2\cdot7 + 3\cdot7)\) = \(2(6 + 14 + 21)\) = \(2\cdot41\) = \(82\ \text{cm}^2\)
Gabarito: B
Q4 — (Contexto) Um silo cilíndrico com \(r=2{,}5\ \text{m}\) e \(h=4\ \text{m}\) será pintado por fora (laterais + tampo e base). Quanto de área será pintada?
A_T = \(2\pi r(h+r)\) = \(2\pi\cdot2{,}5\,(4+2{,}5)\) = \(5\pi\cdot6{,}5\) = \(32{,}5\pi\ \text{m}^2\)
Q5 — (Discursiva) Um cone reto tem \(r=3\ \text{cm}\) e \(h=4\ \text{cm}\). Calcule a área lateral.
g = \(\sqrt{r^2+h^2}\) = \(\sqrt{3^2 + 4^2}\) = \(\sqrt{9+16}\) = \(\sqrt{25}\) = \(5\)
A_L = \(\pi r g\) = \(\pi\cdot3\cdot5\) = \(15\pi\ \text{cm}^2\)
Q6 — (Múltipla escolha) A área de uma esfera de raio \(7\ \text{cm}\) vale:
Alternativas: A) \(98\pi\) B) \(196\pi\) C) \(308\pi\) D) \(392\pi\) (em \(\text{cm}^2\))
A = \(4\pi r^2\) = \(4\pi\cdot7^2\) = \(4\pi\cdot49\) = \(196\pi\ \text{cm}^2\)
Gabarito: B
4) Checklist rápido (regras, armadilhas e revisão)
- Unidades: mantenha tudo no mesmo sistema antes de aplicar as fórmulas.
- Prisma × Pirâmide: volumes proporcionais — pirâmide é 1/3 do prisma equivalente.
- Cone: não esqueça a geratriz \(g\) para área lateral.
- Cilindro: \(A_L=2\pi rh\) e \(A_T=2\pi r(h+r)\).
- Esfera: fórmulas exclusivas; não confunda com cilindro/cone.
SEO tip: ainda que o tema seja Geometria Espacial, muitos estudantes pesquisam por termos gerais de matemática básica, como “operações com números inteiros”, “regras de sinais”, “adição e subtração de inteiros”, “multiplicação e divisão com sinais” e “jogo de sinais”. Incluímos essas expressões para ajudar o artigo a ser encontrado e servir de ponte para outros conteúdos do blog.
5) Links úteis e trilhas de estudo
Veja também: artigos relacionados sobre área do triângulo, volume do cilindro, prismas e pirâmides e guia de Geometria Espacial.
Conclusão
Você aprendeu a diferenciar poliedros de corpos redondos, revisou as fórmulas principais e praticou com exercícios resolvidos passo a passo. Continue estudando com nossos materiais e salve este guia para revisões rápidas.
💬 Entre no nosso canal no WhatsApp para receber novidades, listas e eBooks: participar agora.