Poliedros são sólidos geométricos formados por vértices, arestas e faces, cujas superfícies são polígonos
planos (triângulos, quadriláteros, pentágonos, etc.). A palavra poliedro vem do grego antigo, em que poli
significa ‘’vários’’ e ‘’edros’’ significa ‘’faces’’. Veja alguns exemplos de poliedros:

Relação de Euler
Em um poliedro, como dito antes, podemos distinguir faces, arestas e os vértices. Observe abaixo:
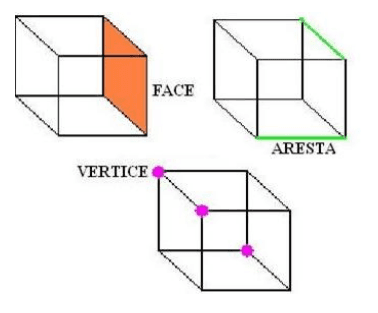
Ou seja:
- faces são as superfícies planas poligonais que limitam o poliedro.
- arestas são as interseções entre as faces do poliedro.
- vértices são os pontos de encontro das arestas.
Leonhard Euler foi um matemático suíço que desenvolveu uma expressão matemática que descreve a relação
entre o número de vértices, arestas e faces de um poliedro convexo. Eis a fórmula:
V + F = A +2
Devemos ter cuidado ao usar essa fórmula, pois ela funciona para qualquer poliedro convexo e para alguns
poliedros côncavos. Mas o que são poliedros convexos e côncavo
- Um poliedro é chamado convexo quando o plano que contém cada face deixa todas as outras em um mesmo
- semiespaço.
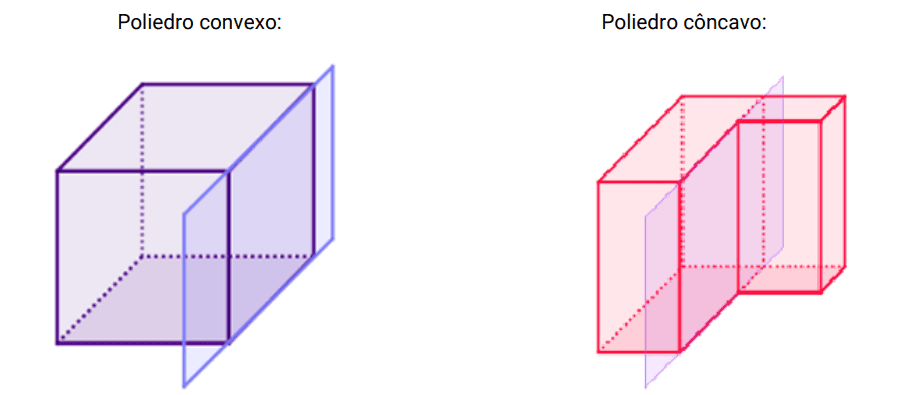
Cálculo para quantidade de arestas de um poliedro
Seja um poliedro com f3 faces triangulares, f4 faces quadrangulares, f5 pentagonais etc.
Podemos calcular a quantidade de arestas (A) desse poliedro usando a fórmula:
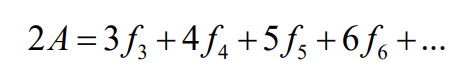
Poliedros de Platão
O filósofo Platão criou um teorema que nos diz que existem 5, e apenas 5, poliedros regulares. Esses 5
poliedros são chamados poliedros de Platão.
Para que possa ser um poliedro de Platão, é necessário que o poliedro obedeça às seguintes disposições:
- todas as faces devem ter a mesma quantidade n de arestas;
- todos os vértices devem ser formados pela mesma quantidade m de arestas;
Estes são os poliedros de Platão:
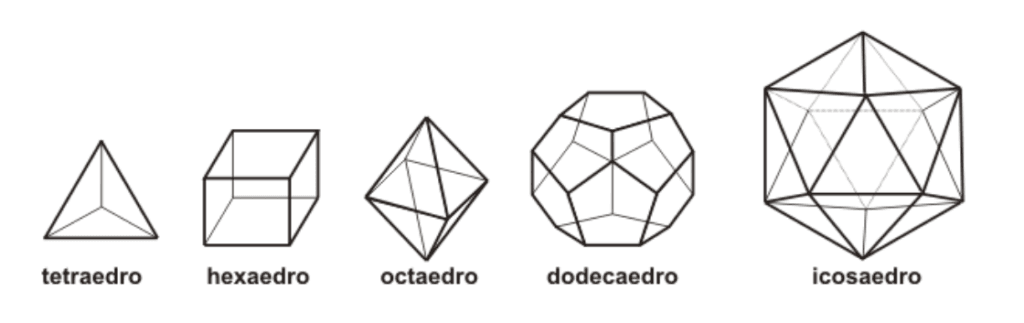
Lista de Exercício Poliedro
1 – O hábito cristalino é um termo utilizado por mineralogistas para descrever a aparência típica de um
cristal em termos de tamanho e forma. A granada é um mineral cujo hábito cristalino é um poliedro
com 30 arestas e 20 vértices. Um mineralogista construiu um modelo ilustrativo de um cristal de
granada pela junção dos polígonos correspondentes às faces. Supondo que o poliedro ilustrativo de
um cristal de é convexo, então a quantidade de faces utilizadas na montagem do modelo ilustrativo
desse cristal é igual a
a) 10.
b) 12.
c) 25.
d) 42.
e) 50.
2 – Um lapidador recebeu de um joalheiro a encomenda para trabalhar em uma pedra preciosa cujo formato
é o de uma pirâmide, conforme ilustra a Figura 1. Para tanto, o lapidador fará quatro cortes de formatos
iguais nos cantos da base. Os cantos retirados correspondem a pequenas pirâmides, nos vértices P, Q,
R e S, ao longo dos segmentos tracejados, ilustrados na Figura 2.
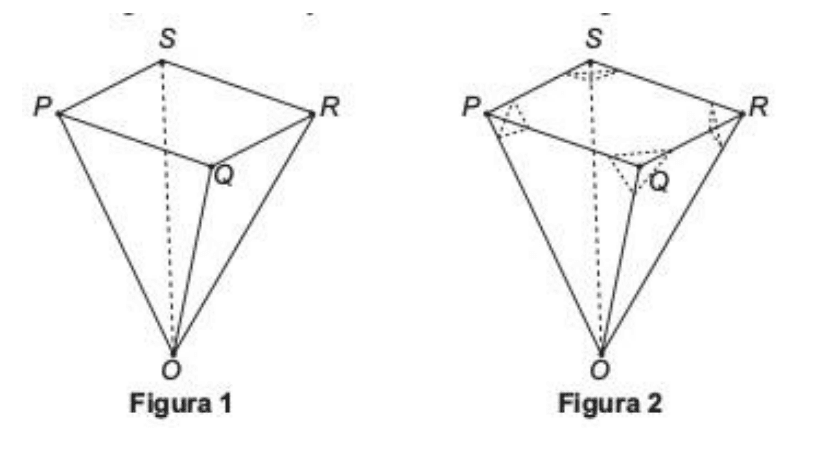
Depois de efetuados os cortes, o lapidador obteve, a partir da pedra maior, uma joia poliédrica cujos
números de faces, arestas e vértices são, respectivamente, iguais a
a) 9, 20 e 13.
b) 9, 24 e 13.
c) 7, 15 e 12.
d) 10, 16 e 5.
e) 11, 16 e 5.
3 – Dois dados, com doze faces pentagonais cada um, têm a forma de dodecaedros regulares. Se os
dodecaedros estão justapostos por uma de suas faces, que coincidem perfeitamente, formam um
poliedro côncavo, conforme ilustra a figura.
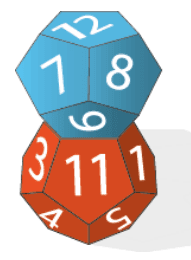
Considere o número de vértices V, de faces F e de arestas A desse poliedro côncavo.
A soma V + F + A é igual a:
a) 102
b) 106
c) 110
d) 112
e) 114
4 – Um icosaedro regular tem 20 faces e 12 vértices, a partir dos quais retiram-se 12 pirâmides
congruentes. As medidas das arestas dessas pirâmides são iguais a 1/3 da aresta do icosaedro. O que
resta é um tipo de poliedro usado na fabricação de bolas. Observe as figuras.
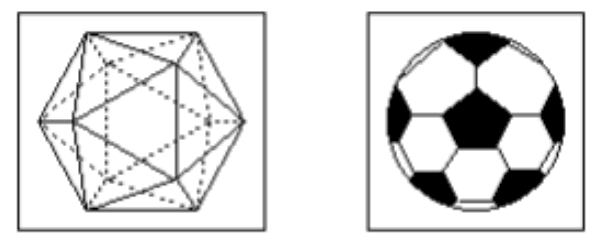
Para confeccionar uma bola de futebol, um artesão usa esse novo poliedro, no qual cada gomo é uma
face. Ao costurar dois gomos para unir duas faces do poliedro, ele gasta 7 cm de linha. Depois de pronta
a bola, o artesão gastou, no mínimo, um comprimento de linha igual a:
a) 7,0 m
b) 6,3 m
c) 4,9 m
d) 2,1 m
5 – Indique quantas faces possuem, respectivamente, nessa ordem, os sólidos numerados como I, II, III e
IV a seguir:

a) 8, 6, 5, 6.
b) 8, 6, 6, 5.
c) 8, 5, 6, 6.
d) 5, 8, 6, 6.
e) 6, 18, 6, 5.
6 – Sobre as sentenças:
I. Um octaedro regular tem 8 faces quadradas.
II. Um dodecaedro regular tem 12 faces pentagonais.
III. Um icosaedro regular tem 20 faces triangulares.
É correto afirmar que a
a) I é verdadeira.
b) II é verdadeira.
c) III é verdadeira.
d) I e II são verdadeiras.
e) II e III são verdadeiras.
7 – Um poliedro convexo apresenta faces quadrangulares e triangulares. Calcule o número de faces desse
poliedro, sabendo que o número de arestas é o quádruplo do número de faces triangulares e o número
de faces quadrangulares é cinco.
a) 8
b) 9
c) 10
d) 11
e) 12
8 – Um poliedro convexo possui duas faces pentagonais e cinco quadrangulares. O número de vértices
deste poliedro é:
a) 4
b) 6
c) 8
d) 9
e) 10
9 – Os sólidos de Platão são poliedros convexos cujas faces são todas congruentes a um único polígono
regular, todos os vértices têm o mesmo número de arestas incidentes e cada aresta é compartilhada
por apenas duas faces. Eles são importantes, por exemplo, na classificação das formas dos cristais
minerais e no desenvolvimento de diversos objetos. Como todo poliedro convexo, os sólidos de Platão
respeitam a relação de Euler V – A + F = 2, em que V, A e F são os números de vértices, arestas e faces
do poliedro, respectivamente.
Em um cristal, cuja forma é a de um poliedro de Platão de faces triangulares, qual é a relação entre o
número de vértices e o número de faces?
a) 2V – 4F = 4
b) 2V – 2F = 4
c) 2V – F = 4
d) 2V + F = 4
e) 2V + 5V = 4
10 – Um poliedro convexo com 32 vértices possui apenas faces triangulares. O número de arestas deste
poliedro é
a) 100
b) 120
c) 90
d) 80
Gabarito
1 – B
2 – A
3 – D
4 – B
5 – A
6 – E
7 – B
8 – E
9 – C
10 – C

























