O conceito de semelhança entre polígonos é essencial na geometria. Ele permite que identifiquemos figuras com a mesma forma, ainda que com tamanhos diferentes. Isso se aplica desde mapas e desenhos técnicos até escalas de modelos arquitetônicos. Mas como saber se dois polígonos são realmente semelhantes?
✅ Os ângulos correspondentes são congruentes (mesma medida);
✅ Os lados correspondentes são proporcionais.
Exemplo com pentágonos QRSTU e ABCDE
Veja a comparação entre dois pentágonos abaixo:
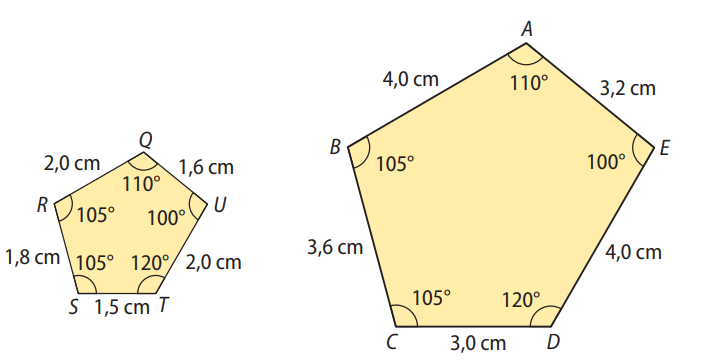
Os ângulos internos dos pentágonos têm as mesmas medidas e aparecem na mesma ordem, ou seja, são congruentes. Os lados correspondentes também mantêm uma razão comum. Isso confirma que os polígonos são semelhantes.
Verificação da Semelhança
Para verificar se os polígonos são semelhantes, siga os passos:
- Compare os ângulos correspondentes. Todos devem ter a mesma medida.
- Compare os lados correspondentes. A razão entre os lados deve ser constante.
No exemplo, temos:
- QR / AB = 2,0 / 4,0 = 1/2
- RS / BC = 1,8 / 3,6 = 1/2
- ST / CD = 1,5 / 3,0 = 1/2
- TU / DE = 2,0 / 4,0 = 1/2
- UQ / EA = 1,6 / 3,2 = 1/2
Como todas as razões são iguais, dizemos que a razão de semelhança é 1/2.
Observações importantes:
- Os lados (ou ângulos) correspondentes também são chamados de homólogos.
- O número que expressa a proporção entre os lados é chamado de razão de semelhança.
- Se dois polígonos semelhantes têm razão de semelhança k, então suas alturas, perímetros e demais medidas lineares também seguem essa razão.
- Se a razão for 1, os polígonos são congruentes.
Importante saber:
Se duas figuras A e B forem semelhantes e a razão de semelhança k for maior que 1, dizemos que A é uma ampliação de B. Se k < 1, A será uma redução de B.
✔️ Ângulos correspondentes são iguais;
✔️ Lados correspondentes estão na mesma proporção.
📚 Para aprofundar seus estudos:
📘 Baixe os 10 eBooks gratuitos de Matemática com teoria e exercícios passo a passo:
👉 Clique aqui para baixar
🧠 Mapas Mentais de Matemática: visualize rapidamente as propriedades dos polígonos e outros temas:
👉 Acesse os mapas aqui
Agora que você entendeu o conceito de polígonos semelhantes, pratique com figuras geométricas variadas e observe a aplicação desse conhecimento em problemas práticos e provas de concursos e vestibulares.
✏️ Indicação de leitura: Entenda o Teorema de Tales com exemplos visuais
Você sabe como aplicar o Teorema de Tales na prática? Neste artigo você vai entender o conceito de forma simples, com imagens e exercícios resolvidos passo a passo.
👉 Acessar o artigo completo🟣 Exercício Resolvido – Polígonos Semelhantes
Enunciado:
Os pentágonos ABCDE e MNOPQ são semelhantes. Sabendo que o perímetro do pentágono ABCDE é 8,7 cm, determine a medida de seus lados.
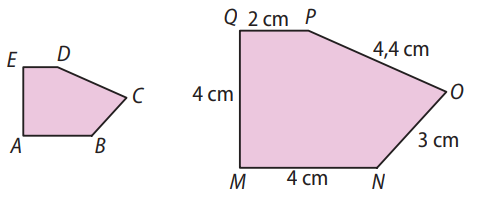
Resolução:
Como os pentágonos são semelhantes, os lados correspondentes estão na mesma proporção.
As medidas dos lados do pentágono MNOPQ são:
- MN = 4 cm
- NO = 4,4 cm
- OP = 3 cm
- PQ = 2 cm
- QM = 4 cm
O perímetro de MNOPQ é a soma desses lados:
P(MNOPQ) = 4 + 4,4 + 3 + 2 + 4 = 17,4 cm
A razão de semelhança entre os pentágonos será a razão entre os perímetros:
k = P(ABCDE) ÷ P(MNOPQ) = 8,7 ÷ 17,4 = 1/2
Como a razão é 1/2, os lados do pentágono ABCDE serão metade dos lados de MNOPQ.
Calculando os lados correspondentes:
- AB = MN ÷ 2 = 4 ÷ 2 = 2,0 cm
- BC = NO ÷ 2 = 4,4 ÷ 2 = 2,2 cm
- CD = OP ÷ 2 = 3 ÷ 2 = 1,5 cm
- DE = PQ ÷ 2 = 2 ÷ 2 = 1,0 cm
- EA = QM ÷ 2 = 4 ÷ 2 = 2,0 cm
Resposta final:
As medidas dos lados do pentágono ABCDE são: 2,0 cm, 2,2 cm, 1,5 cm, 1,0 cm e 2,0 cm.













