Em uma reta orientada \(r\), escolhemos um ponto origem \(O\) e marcamos uma unidade. Assim, cada ponto passa a ter uma abscissa (um número real) que mede sua posição em relação a \(O\). Esse é o embrião do eixo real do plano cartesiano. Veja também: ENEM Matemática, Mapas Mentais e o Banco de Questões.

Vocabulário essencial

Exemplos rápidos

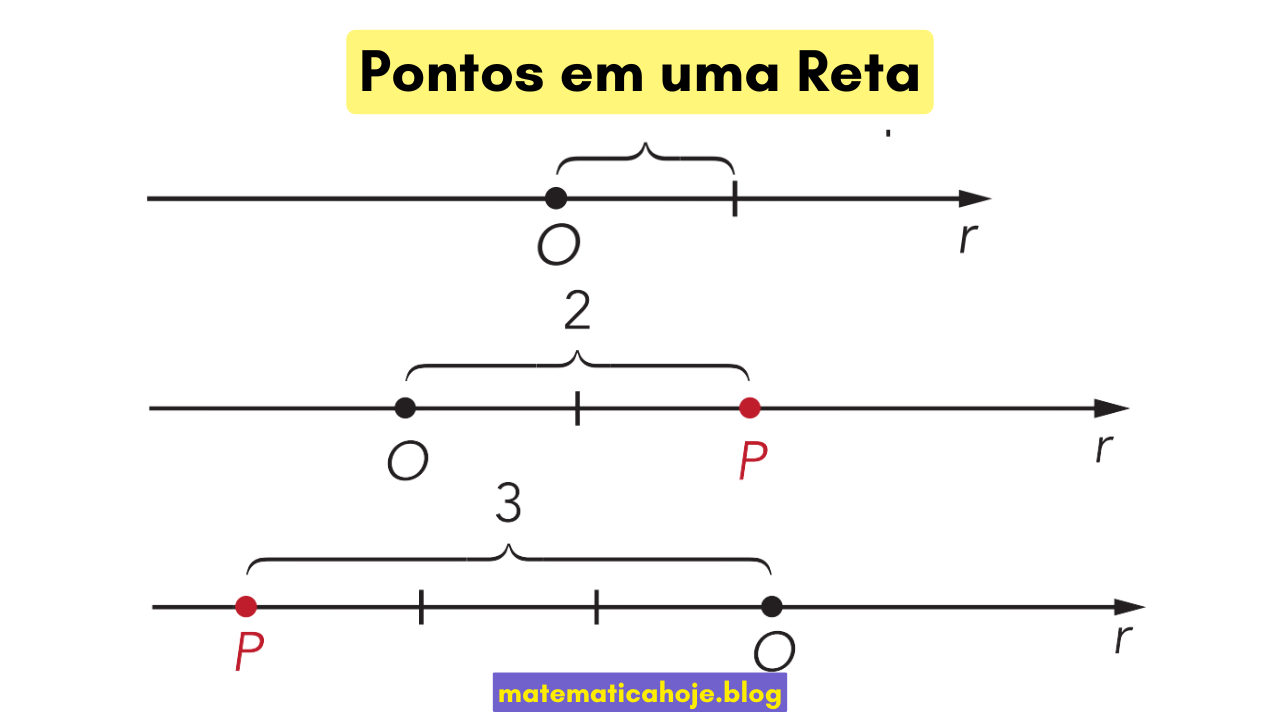
Exemplo 1 — Abscissa pelo desenho

Na figura, o ponto \(P\) está a 2 unidades à direita de \(O\) (no segundo esquema): \(x_P=+2\). No terceiro, \(P\) está 3 unidades à esquerda de \(O\): \(x_P=-3\).

Exemplo 2 — Distância sobre a reta

Se \(A(-4)\) e \(B(3)\), então \(AB=|3-(-4)|=7\).

Exemplo 3 — Ponto médio

Para \(A(1)\) e \(B(7)\): \(M=\dfrac{1+7}{2}=4\).

Exemplo 4 — Dividir \(AB\) na razão \(2:3\)

Com \(A(0)\) e \(B(10)\): \(P=\dfrac{2\cdot10+3\cdot0}{2+3}=4\). O ponto \(P\) fica mais próximo de \(A\) (maior peso para \(B\)).

Exercícios (múltipla escolha) com solução

1) Se \(x_A=-2\) e \(x_B=5\), a distância \(AB\) vale:

1. 3
2. 5
3. 7
4. 9

2) O simétrico de \(P(3{,}5)\) em relação à origem é:

1. \(-3{,}5\)
2. \(3{,}5\)
3. \(0\)
4. \(7\)

3) Se \(A(-1)\) e \(B(9)\), o ponto médio \(M\) tem abscissa:

1. 3
2. 4
3. 5
4. 6

4) No eixo real, qual é o conjunto dos pontos \(x\) a distância 3 do ponto \(2\)?

1. \(\{5\}\)
2. \(\{-1,5\}\)
3. \(\{-1\}\)
4. \(\{3,\, -3\}\)

5) Divida o segmento de \(A(2)\) a \(B(12)\) na razão \(1:4\) (mais próximo de \(A\)). A abscissa do ponto é:

1. 4
2. 6
3. 10
4. 11

6) Se \(x_M=1\) é o ponto médio de \(A(-7)\) e \(B(x)\), então \(x\) é:

1. \(5\)
2. \(7\)
3. \(9\)
4. \(11\)

Para continuar estudando

• Mapas Mentais de Matemática
• Coleção 10 eBooks de Matemática
• Banco de Questões Matemática
• Roteiro de Matemática para o ENEM