Matemática Hoje • Potenciação
Potenciação: como dominar expoentes com exemplos e exercícios?
A potenciação é uma forma rápida de multiplicar uma base por ela mesma várias vezes. Neste guia, você entenderá o conceito, as propriedades clássicas (produto, quociente, potência de potência, potência de produto, expoente zero e negativo), verá exemplos práticos e treinará com exercícios comentados no estilo ENEM.
📘 Baixe grátis: eBook de Fórmulas Matemáticas
PDF enxuto para revisar potência, radiciação, logaritmos, PA/PG, geometria e estatística.
Definição de potência e leitura de expoentes
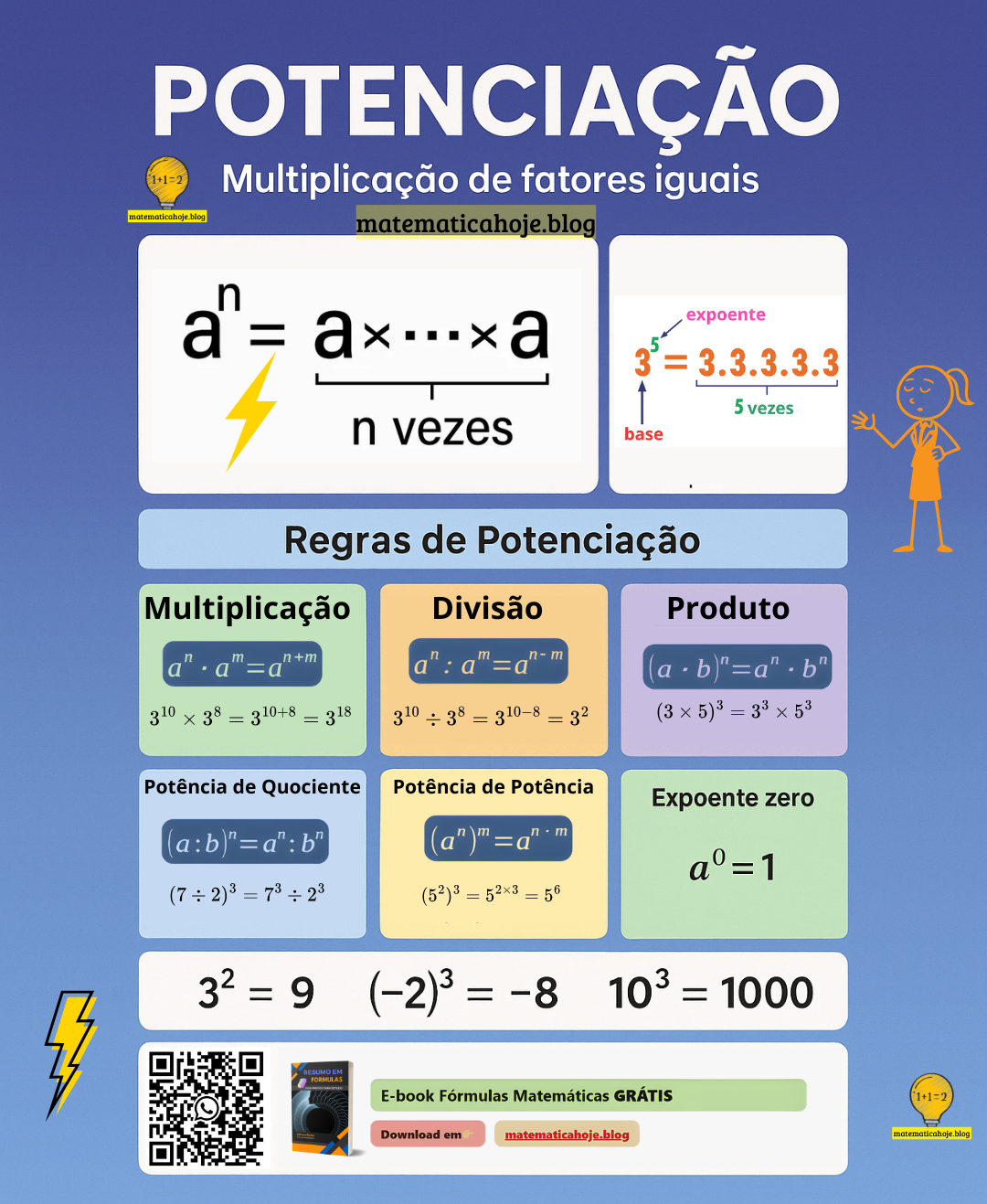
Potenciação escreve multiplicações repetidas da mesma base. Notação: $a^n$. Lemos “a elevado a n”.
Definição: para $a\in\mathbb{R}$ e $n\in\mathbb{N}$, $a^n=\underbrace{a\cdot a\cdot \dots \cdot a}_{n\text{ fatores}}$.
Casos especiais: $a^1=a$, $a^0=1$ (com $a\neq0$) e $a^{-n}=\dfrac{1}{a^n}$.
Exemplo prático: contagem de dobras de papel
Ao dobrar um papel, o número de camadas segue $2^n$. Em 1, 2 e 3 dobras, temos 2, 4 e 8 camadas, respectivamente.
Regras e propriedades dos expoentes (essenciais)
- Produto: $a^m\cdot a^n=a^{m+n}$
- Quociente: $\dfrac{a^m}{a^n}=a^{m-n}$ ($a\neq0$)
- Potência de potência: $(a^m)^n=a^{mn}$
- Potência de produto: $(ab)^n=a^n b^n$
- Expoente zero: $a^0=1$ ($a\neq0$)
- Expoente negativo: $a^{-n}=\dfrac{1}{a^n}$
Erros comuns para evitar
- Confundir $a^m+a^n$ com $a^{m+n}$. Somar potências ≠ multiplicá-las.
- Esquecer que $a^0=1$ ($a\neq0$).
- Aplicar “regra da soma” no expoente: em geral, $(a+b)^n\neq a^n+b^n$.
Potências de 10, notação científica e grandezas
Potências de 10 agilizam cálculos e padronizam medidas muito grandes ou muito pequenas.
Notação científica: $N=c\cdot 10^k$, com $1\le c<10$ e $k\in\mathbb{Z}$.
Exemplo aplicado
$0{,}00032=3{,}2\cdot 10^{-4}$ e $5\,800\,000=5{,}8\cdot 10^{6}$.
🧠 Mapas Mentais de Matemática (Potenciação e mais)
Visualize as regras de expoentes em uma página resumida, ótima para revisão rápida.
Relação entre potenciação e radiciação
A radiciação é a operação inversa da potenciação. Para $n\in\mathbb{N}$, $\sqrt[n]{a}=a^{\tfrac{1}{n}}$ (com hipóteses usuais sobre $a$).
Exemplo com passos em forma matemática
Exemplos trabalhados com expoentes (passo a passo)
Exemplo 1 — simplificação com produto de potências
Exemplo 2 — quociente e expoente negativo
Exemplo 3 — potência de potência
Exemplo 4 — potência de produto
📘 Reforço rápido: eBook de Fórmulas (PDF)
Revise potenciação, radiciação, logaritmos e mais com um material direto ao ponto.
Lista de exercícios sobre potenciação (com soluções)
1) Simplificação direta com produto de potências
Enunciado: Simplifique $3^4\cdot 3^2$.
👀 Ver solução passo a passo
2) Quociente de potências com mesma base
Enunciado: Calcule $\dfrac{7^9}{7^3}$.
👀 Ver solução passo a passo
Se desejar o valor numérico: $7^6=117\,649$.
3) Expoente negativo e reciprocidade
Enunciado: Escreva $4^{-3}$ como fração.
👀 Ver solução passo a passo
4) Potência de potência (com número grande)
Enunciado: Simplifique $(10^2)^5$.
👀 Ver solução passo a passo
Valor: $10^{10}=10\,000\,000\,000$.
5) Potência de produto (separe fatores)
Enunciado: Calcule $(6\cdot 5)^2$ usando as propriedades.
👀 Ver solução passo a passo
6) Notação científica e potência de 10
Enunciado: Escreva $0{,}000072$ em notação científica.
👀 Ver solução passo a passo
7) Misturando propriedades (produto + quociente)
Enunciado: Simplifique $\dfrac{2^8\cdot 2^3}{2^5}$.
👀 Ver solução passo a passo
8) Expoente fracionário (ligação com raiz)
Enunciado: Calcule $27^{\tfrac{2}{3}}$.
👀 Ver solução passo a passo
Conclusão: como fixar potenciação de forma inteligente
Para dominar potenciação, pratique as propriedades diariamente, resolva exercícios variados e valide seus resultados. Use potências de 10 para estimar e converter medidas com agilidade. Depois, avance para logaritmos e PG. Reforce com os Mapas Mentais e o eBook de Fórmulas.
FAQ — dúvidas frequentes sobre potenciação
1) O que significa elevar um número a um expoente?
Elevar é repetir multiplicações da mesma base. Em $a^n$, multiplica-se $a$ por ele mesmo $n$ vezes. Essa notação simplifica cálculos e aparece em medidas, ciências e finanças.
2) Quais são as principais propriedades dos expoentes?
Produto e quociente de potências de mesma base, potência de potência, potência de produto, expoente zero e expoente negativo. Com elas, é possível simplificar expressões rapidamente.
3) Como funcionam potências de 10 na prática?
Servem para escrever números muito grandes ou pequenos em notação científica; por exemplo, $3{,}5\cdot 10^6$ e $8{,}1\cdot 10^{-4}$. Ajudam em estimativas e conversões rápidas.
4) Qual a relação entre potenciação e radiciação?
São operações inversas. A raiz enésima equivale ao expoente fracionário $1/n$, o que simplifica cálculos como $a^{\tfrac{p}{q}}=(\sqrt[q]{a})^p$.
5) Onde praticar exercícios de potenciação no estilo ENEM?
No Banco de Questões e na página do ENEM Matemática, com itens comentados, dicas e simulados.
Autor: Adriano Rocha • Matemática Hoje

























