Prisma Pentagonal — guia completo
Tudo sobre prisma de base pentagonal: definição, elementos, fórmulas, planificação, caso regular, exemplos com contas na vertical e exercícios.
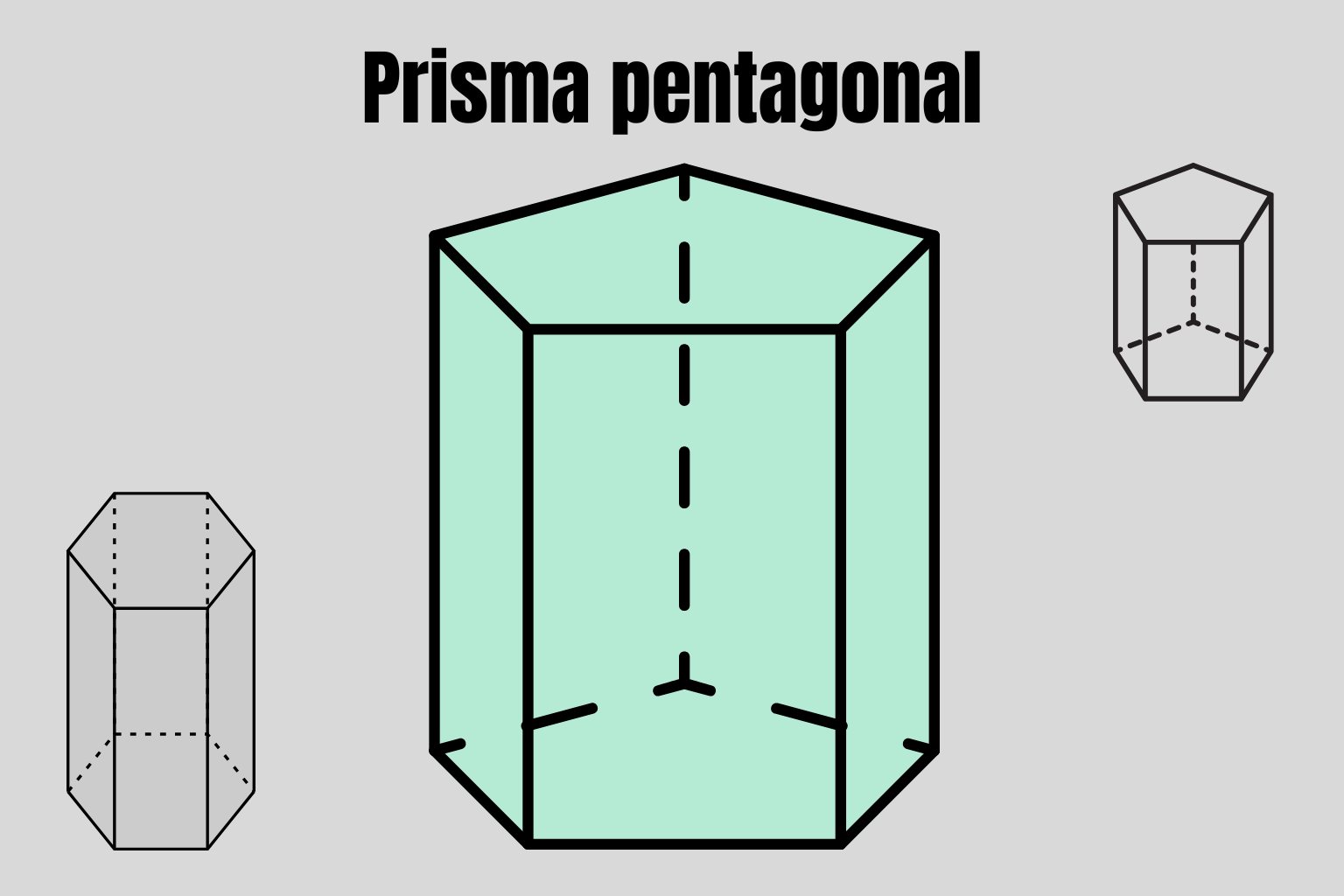
1) O que é um prisma pentagonal?
Prisma pentagonal é o prisma cujas bases são pentágonos congruentes e as faces laterais são cinco retângulos. Em prisma reto, a altura do prisma coincide com a aresta lateral \(h\).
- Perímetro da base: \(p\)
- Área de uma base: \(A_b\)
- Altura do prisma: \(h\)
- Contagem: Faces = 7, Arestas = 15, Vértices = 10 (checa Euler: \(10-15+7=2\)).
Relembre: Poliedros e Fórmula de Euler.
2) Fórmulas (atenção ao tipo de prisma)
Em prismas retos, \(g=h\). Em oblíquos, \(g\neq h\) em geral.
3) Prisma pentagonal regular (base pentágono regular)
Para base regular (lado \(a\), apótema \(r\)):
- \(p=5a\)
- \(A_b=\dfrac{p\,r}{2}=\dfrac{5a\,r}{2}\)
- Sem apótema: \(A_b=\dfrac{a^2}{4}\sqrt{25+10\sqrt5}\)
- Consequências: \(A_L=5a\,h,\ \ A_T=5a\,h+2A_b,\ \ V=A_b\,h\)
Equivalente útil: \(r=\dfrac{a}{2}\cot 36^\circ=\dfrac{a}{2\tan 36^\circ}\). Revise triângulos semelhantes e prismas regulares.
4) Planificação do prisma pentagonal
A planificação contém 5 retângulos (faixa lateral \(p\times h\)) e 2 pentágonos (bases). Ao somar as áreas dos 5 retângulos, obtemos diretamente \(A_L=p\,h\) no caso reto.
Veja também: Planificação do Cubo e Planificação do Paralelepípedo.
5) Exemplos resolvidos
Exemplo 1 — Enfeite de coluna (prisma pentagonal regular: a = 10 cm, h = 12 cm)
Situação-problema. Um enfeite que reveste uma coluna tem forma de prisma pentagonal regular. O lado do pentágono é 10 cm e a altura do prisma é 12 cm. Para estimar o material, calcule a área total e o volume do enfeite.
Solução (vertical).
$$\begin{aligned} p &= 5a\\ &= 5\cdot 10\\ &= 50\\[6pt] A_b &= \frac{a^2}{4}\sqrt{25+10\sqrt5}\\ &= \frac{100}{4}\sqrt{25+10\sqrt5}\\ &= 25\sqrt{25+10\sqrt5}\\[6pt] A_L &= p\cdot h\\ &= 50\cdot 12\\ &= 600\ \text{cm}^2\\[6pt] A_T &= A_L + 2A_b\\ &= 600 + 2\cdot 25\sqrt{25+10\sqrt5}\\ &= \boxed{600 + 50\sqrt{25+10\sqrt5}\ \text{cm}^2}\\[6pt] V &= A_b\cdot h\\ &= 25\sqrt{25+10\sqrt5}\cdot 12\\ &= \boxed{300\sqrt{25+10\sqrt5}\ \text{cm}^3} \end{aligned}$$Aproximação: \(\sqrt{25+10\sqrt5}\approx 6{,}8820\). Assim, \(A_b\approx 172{,}05\ \text{cm}^2\), \(A_T\approx 944{,}10\ \text{cm}^2\), \(V\approx 2\,064{,}6\ \text{cm}^3\).
Exemplo 2 — Reservatório decorativo (regular: a = 8 cm, apótema r = 5,5 cm, h = 20 cm)
Situação-problema. Um reservatório decorativo é um prisma pentagonal regular. O lado da base mede 8 cm, o apótema do pentágono é 5,5 cm e a altura do prisma é 20 cm. Calcule a área total a ser envernizada e o volume interno.
Solução (vertical).
$$\begin{aligned} p &= 5a\\ &= 5\cdot 8\\ &= 40\\[6pt] A_b &= \frac{p\,r}{2}\\ &= \frac{40\cdot 5{,}5}{2}\\ &= \frac{220}{2}\\ &= 110\ \text{cm}^2\\[6pt] A_L &= p\cdot h\\ &= 40\cdot 20\\ &= 800\ \text{cm}^2\\[6pt] A_T &= A_L + 2A_b\\ &= 800 + 2\cdot 110\\ &= \boxed{1\,020\ \text{cm}^2}\\[6pt] V &= A_b\cdot h\\ &= 110\cdot 20\\ &= \boxed{2\,200\ \text{cm}^3} \end{aligned}$$Como usamos \(A_b=\dfrac{pr}{2}\), os valores já são exatos.
Exemplo 3 — Tampa de caixa (base qualquer: lados 7, 8, 9, 8, 8 cm; h = 15 cm)
Situação-problema. Uma tampa de caixa tem a forma de um prisma pentagonal, mas a base não é regular — seus lados medem 7, 8, 9, 8, 8 cm. A altura do prisma é 15 cm. Após medir no projeto, obteve-se a área da base por decomposição: \(A_b=142\ \text{cm}^2\). O perímetro é \(p=40\ \text{cm}\). Determine a área total de material e o volume.
Solução (vertical).
$$\begin{aligned} A_L &= p\cdot h\\ &= 40\cdot 15\\ &= 600\ \text{cm}^2\\[6pt] A_T &= A_L + 2A_b\\ &= 600 + 2\cdot 142\\ &= \boxed{884\ \text{cm}^2}\\[6pt] V &= A_b\cdot h\\ &= 142\cdot 15\\ &= \boxed{2\,130\ \text{cm}^3} \end{aligned}$$Quando a base não é regular, calcule \(A_b\) por decomposição em triângulos (ou coordenadas/GEO) e use \(A_L=p\,h\) no prisma reto.
Exemplo 3 — Base qualquer (lados 7, 8, 9, 8, 8 cm), h = 15 cm
Supondo que a decomposição da base em triângulos forneça \(A_b=142\ \text{cm}^2\) e o perímetro seja \(p=40\ \text{cm}\):
$$\begin{aligned} A_L &= p\cdot h\\ &= 40\cdot 15\\ &= 600\ \text{cm}^2\\[6pt] A_T &= A_L + 2A_b\\ &= 600 + 2\cdot 142\\ &= \boxed{884\ \text{cm}^2}\\[6pt] V &= A_b\cdot h\\ &= 142\cdot 15\\ &= \boxed{2\,130\ \text{cm}^3} \end{aligned}$$Aproximações: valores já numéricos — \(A_T=884\ \text{cm}^2\), \(V=2\,130\ \text{cm}^3\).
6) Exercícios propostos
- Prisma pentagonal regular com \(a=6\ \text{cm}\) e \(h=18\ \text{cm}\). Calcule \(A_L\), \(A_T\) e \(V\).
- Prisma pentagonal regular: \(a=12\ \text{cm}\), \(r=8\ \text{cm}\), \(h=25\ \text{cm}\). Calcule \(A_b\), \(A_T\) e \(V\).
- Um prisma pentagonal tem \(p=52\ \text{cm}\), \(A_b=160\ \text{cm}^2\) e \(h=14\ \text{cm}\). Calcule \(A_L\), \(A_T\) e \(V\).
- Planificação: base regular com \(a=10\ \text{cm}\) e \(h=30\ \text{cm}\). Dê as dimensões da faixa lateral e a área da chapa (sem abas).
- (Aplicado) Uma caixa em forma de prisma pentagonal regular \(a=5\ \text{cm}\), \(h=20\ \text{cm}\) será pintada por fora. O custo é R$ 45,00/m². Calcule o custo total de pintura.
Quer as soluções na vertical e versão em múltipla escolha? Posso gerar no mesmo padrão dos nossos exercícios.
7) Perguntas rápidas
É sólido de Platão? Não. Veja Sólidos de Platão.
Como obter o apótema \(r\) do pentágono regular? \(r=\dfrac{a}{2}\cot 36^\circ=\dfrac{a}{2\tan 36^\circ}\). Então \(A_b=\dfrac{5ar}{2}\).






















