Prisma Reto — Volume e Áreas (com Exercícios)
Resumo claro com fórmulas, exemplos passo a passo (as contas ficam em linhas separadas) e exercícios de treino.
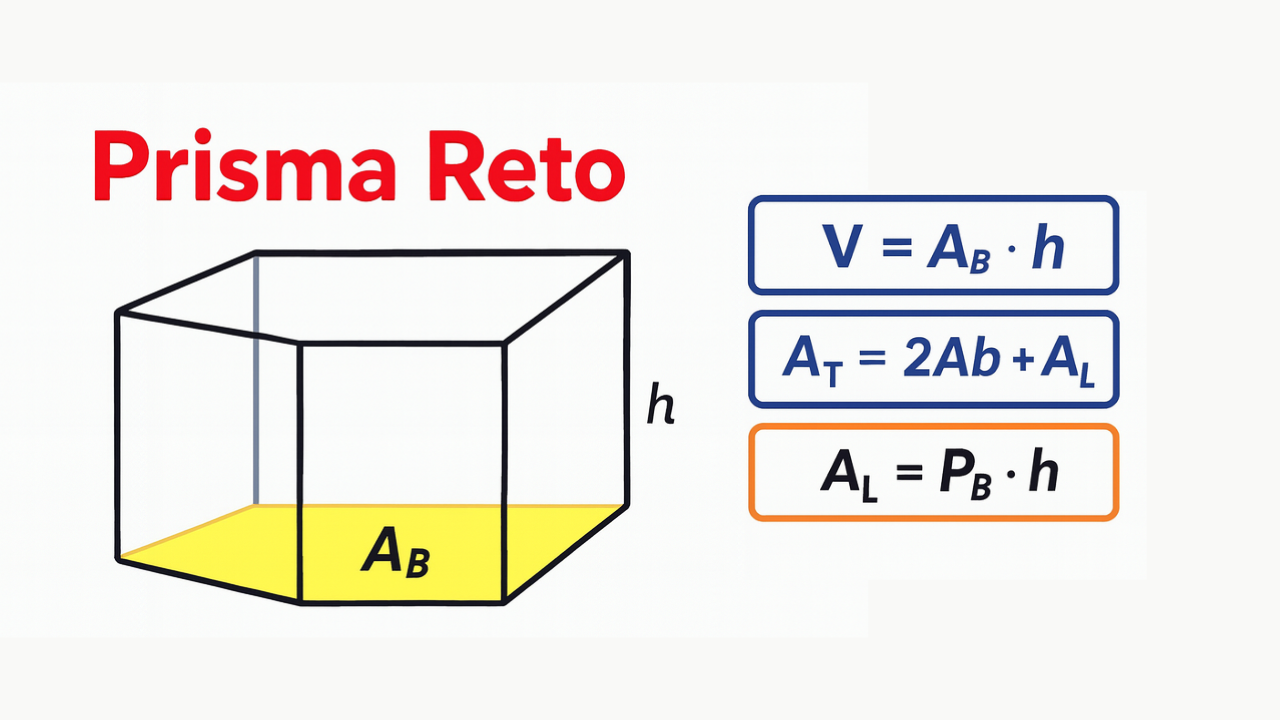
O que é um Prisma Reto?
É um prisma cujas arestas laterais são perpendiculares ao plano da base. Notação usada:
- \(A_B\) — área da base;
- \(P_B\) — perímetro da base;
- \(h\) — altura do prisma (distância entre as bases);
- \(A_L\) — área lateral; \(A_T\) — área total.
Conteúdo frequente no ENEM Matemática. Para memorização, veja os Mapas Mentais de Matemática.
Fórmulas essenciais
Volume
\( V = A_B \cdot h \)
Áreas
Área lateral: \( A_L = P_B \cdot h \) | Área total: \( A_T = 2A_B + A_L \)
Para bases regulares, use as fórmulas conhecidas de \(A_B\) e \(P_B\) (triângulo, quadrado, hexágono, etc.).
Mais prática no Banco de Questões e na Coleção 10 eBooks.
Exemplos resolvidos (passo a passo)
Exemplo 1 — Prisma de base retangular
Enunciado. Base retângulo \(8\,\text{cm}\times 3\,\text{cm}\) e altura \(h=10\,\text{cm}\). Calcule \(V\), \(A_L\) e \(A_T\).
Ver solução
\( A_B = 8\cdot 3 \)
\( = 24\ \text{cm}^2 \)
\( P_B = 2(8+3) \)
\( = 2\cdot 11 \)
\( = 22\ \text{cm} \)
\( V = A_B\cdot h \)
\( = 24\cdot 10 \)
\( = \mathbf{240\ \text{cm}^3} \)
\( A_L = P_B\cdot h \)
\( = 22\cdot 10 \)
\( = \mathbf{220\ \text{cm}^2} \)
\( A_T = 2A_B + A_L \)
\( = 2\cdot 24 + 220 \)
\( = 48 + 220 \)
\( = \mathbf{268\ \text{cm}^2} \)
Exemplo 2 — Prisma de base triangular equilátera
Enunciado. Base: triângulo equilátero de lado \(6\,\text{cm}\). Altura do prisma \(h=12\,\text{cm}\). Encontre \(V\).
Ver solução
\( A_B = \dfrac{\sqrt{3}}{4}\,s^2 \)
\( = \dfrac{\sqrt{3}}{4}\cdot 6^2 \)
\( = \dfrac{\sqrt{3}}{4}\cdot 36 \)
\( = 9\sqrt{3}\ \text{cm}^2 \)
\( V = A_B\cdot h \)
\( = 9\sqrt{3}\cdot 12 \)
\( = 108\sqrt{3} \)
\( \approx \mathbf{187{,}1\ \text{cm}^3} \)
Exemplo 3 — Prisma de base hexagonal regular
Enunciado. Base: hexágono regular de lado \(a=5\,\text{cm}\). Altura \(h=10\,\text{cm}\). Calcule \(A_L\).
Ver solução
\( P_B = 6a \)
\( = 6\cdot 5 \)
\( = 30\ \text{cm} \)
\( A_L = P_B\cdot h \)
\( = 30\cdot 10 \)
\( = \mathbf{300\ \text{cm}^2} \)
📘 eBook Grátis — Fórmulas Matemática
Todas as fórmulas de Geometria Espacial, Planimetria, Álgebra e mais — perfeito para revisão.
➡️ Baixar AgoraExercícios — Prisma Reto
Para mais treino, acesse o Banco de Questões e a Coleção 10 eBooks.
1) Um prisma reto tem base quadrada de lado \(4\) cm e altura \(9\) cm. O volume é:
- 64 cm³
- 96 cm³
- 144 cm³
- 256 cm³
Ver solução
\( = 16 \)
\( V = A_B\cdot h = 16\cdot 9 = \mathbf{144\ \text{cm}^3} \). Alternativa C.
2) Em um prisma reto com base retangular \(5\times 7\) cm e \(h=8\) cm, a área lateral é:
- 96 cm²
- 160 cm²
- 192 cm²
- 240 cm²
Ver solução
\( A_L = P_B\cdot h = 24\cdot 8 = \mathbf{192\ \text{cm}^2} \). Alternativa C.
3) Um prisma de base triangular equilátera de lado \(10\) cm e \(h=15\) cm tem área total:
- 750√3 cm²
- 300√3 + 450 cm²
- 150√3 + 450 cm²
- 300√3 + 300 cm²
Ver solução
\( P_B = 3\cdot 10 = 30 \)
\( A_L = P_B\cdot h = 30\cdot 15 = 450 \)
\( A_T = 2A_B + A_L = 2\cdot 25\sqrt{3} + 450 = \mathbf{50\sqrt{3}+450} \ \text{cm}^2 \). Alternativa C.
4) Se \(A_L=240\) cm² e \(h=12\) cm, então \(P_B\) vale:
- 10 cm
- 12 cm
- 18 cm
- 20 cm
Ver solução
\( = \dfrac{240}{12} \)
\( = \mathbf{20\ \text{cm}} \). Alternativa D.
5) Em um prisma reto, dobrar a altura \(h\) e manter a base fixa faz com que:
- o volume dobre e \(A_L\) dobre
- o volume dobre e \(A_L\) permaneça
- o volume quadruplique
- nada mude
Ver solução
\( A_L = P_B\cdot h \Rightarrow \) também dobra.
Alternativa A.













