Prisma triangular

Prisma Triangular — definição, fórmulas, planificação e exercícios

Prisma Triangular — guia completo

Definição, elementos, fórmulas (área lateral, área total e volume), planificação, casos geral e regular (base equilátera) e exemplos resolvidos com contas na vertical.

Imagem do artigo: Prisma Triangular.

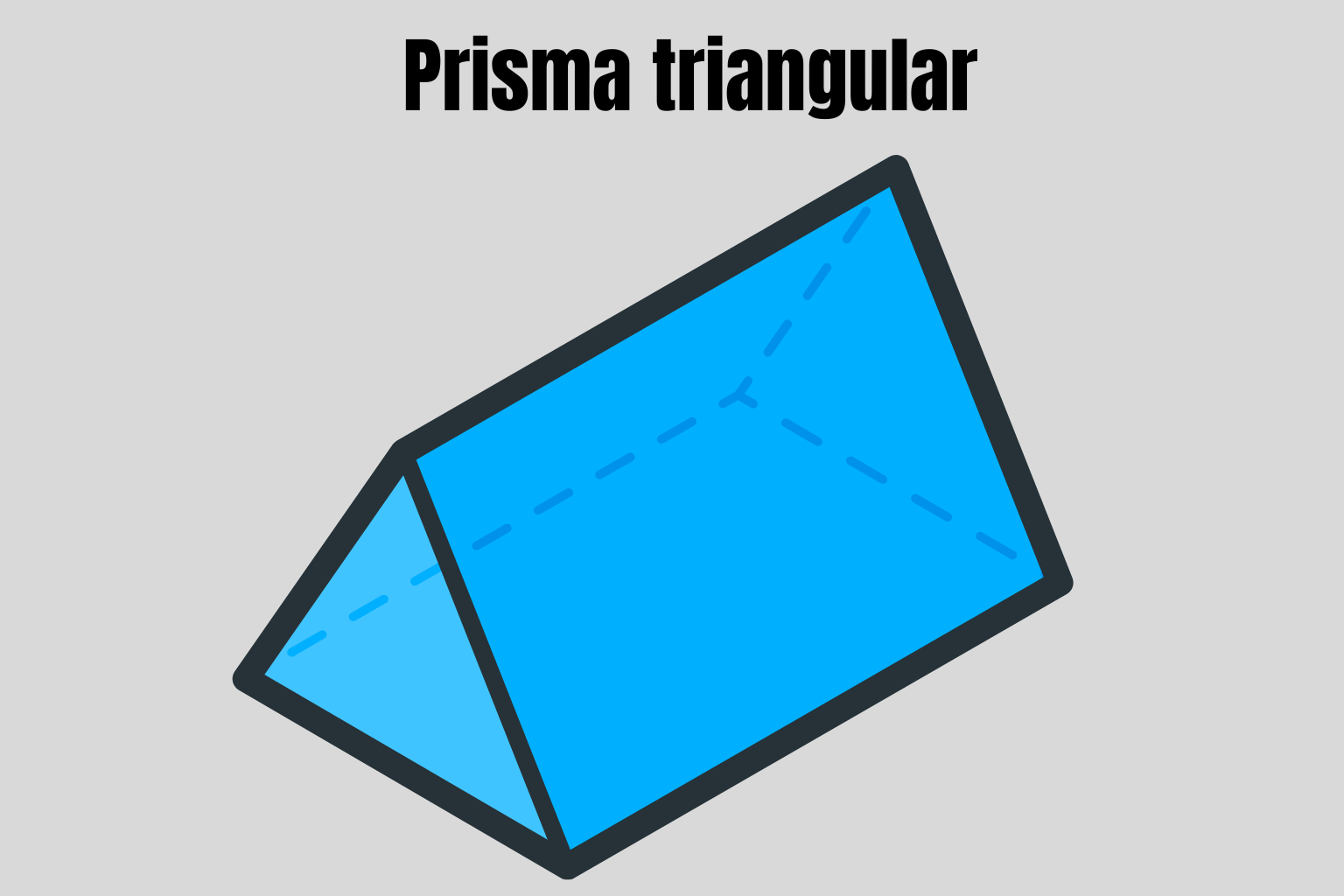
1) O que é um prisma triangular?

Prisma triangular é um prisma cujas bases são triângulos congruentes e as faces laterais são retangulares. Se o prisma for reto, a altura do sólido é a própria aresta lateral $h$.

Perímetro da base: $p$
Área da base: $A_b$ (depende do triângulo da base)
Altura do prisma: $h$

2) Fórmulas essenciais (qualquer prisma triangular)

Área lateral: $A_L = p \cdot h$

Área total: $A_T = A_L + 2A_b$

Volume: $V = A_b \cdot h$

Lembre: $p$ é o perímetro do triângulo da base (soma dos 3 lados). $A_b$ pode ser calculada por: fórmulas de área de triângulo (base×altura/2, Heron, etc.).

3) Como calcular a área da base triangular $A_b$?

Triângulo qualquer (Heron)

Se os lados da base são $a,b,c$:

$s=\dfrac{a+b+c}{2}$ e $A_b=\sqrt{s(s-a)(s-b)(s-c)}$

Casos comuns

Retângulo (catetos $b,c$): $\ A_b=\dfrac{b\,c}{2}$
Equilátero (lado $a$): $\ A_b=\dfrac{\sqrt3}{4}a^2$
Isósceles: use base×altura/2 (altura por Pitágoras) ou Heron

Reforce: triângulo equilátero • triângulo retângulo isósceles • triângulos semelhantes.

4) Prisma triangular regular base equilátera

Se a base é equilátera (lado $a$), então:

$p=3a$
$A_b=\dfrac{\sqrt3}{4}a^2$
$A_L=3a\,h$
$A_T=3a\,h+\dfrac{\sqrt3}{2}a^2$
$V=\dfrac{\sqrt3}{4}a^2\,h$

5) Planificação do prisma triangular

A planificação tem um retângulo de dimensões $p\times h$ (as três faces laterais “abertas”) e duas bases triangulares congruentes. Por isso, $A_L=p\,h$ e $A_T=p\,h+2A_b$.

6) Exemplos resolvidos (abre/fecha)

Exemplo 1 — Prisma triangular regular: área total e volume

Dados: lado da base (equilátera) $a=10\ \text{cm}$, altura do prisma $h=12\ \text{cm}$. Calcule a área total e o volume.

$$\begin{aligned} p&=3a=30\\ A_b&=\frac{\sqrt3}{4}\cdot a^2=\frac{\sqrt3}{4}\cdot100=25\sqrt3\\ A_L&=p\,h=30\cdot12=360\\[2mm] A_T&=A_L+2A_b=360+2\cdot25\sqrt3=\boxed{360+50\sqrt3\ \text{cm}^2}\\[2mm] V&=A_b\,h=25\sqrt3\cdot12=\boxed{300\sqrt3\ \text{cm}^3} \end{aligned}$$

Exemplo 2 — Base retângula (3-4-5): área total e volume

Dados: base triangular retângula com catetos $b=6\ \text{cm}$ e $c=8\ \text{cm}$ (hipotenusa $=10\ \text{cm}$); altura do prisma $h=15\ \text{cm}$. Calcule a área total e o volume.

$$\begin{aligned} A_b&=\frac{b\,c}{2}=\frac{6\cdot8}{2}=24\\ p&=6+8+10=24\\ A_L&=p\,h=24\cdot15=360\\ A_T&=A_L+2A_b=360+2\cdot24=\boxed{408\ \text{cm}^2}\\ V&=A_b\,h=24\cdot15=\boxed{360\ \text{cm}^3} \end{aligned}$$

Exemplo 3 — Base escalena (Heron): área total e volume

Dados: lados da base $a=7\ \text{cm},\ b=9\ \text{cm},\ c=10\ \text{cm}$; altura do prisma $h=20\ \text{cm}$. Calcule a área total e o volume.

$$\begin{aligned} s&=\frac{a+b+c}{2}=\frac{7+9+10}{2}=13\\ A_b&=\sqrt{s(s-a)(s-b)(s-c)}=\sqrt{13\cdot6\cdot4\cdot3}\\ &=\sqrt{936}\ \approx 30{,}595\\ p&=a+b+c=26\\ A_L&=p\,h=26\cdot20=520\\ A_T&=A_L+2A_b\approx 520+2\cdot30{,}595\approx \boxed{581{,}19\ \text{cm}^2}\\ V&=A_b\,h\approx 30{,}595\cdot20\approx \boxed{611{,}90\ \text{cm}^3} \end{aligned}$$

Arredonde conforme a necessidade do problema (1 ou 2 casas decimais).

7) Exercícios (múltipla escolha, com soluções)

1) Prisma triangular regular — área total e volume

Um prisma triangular regular tem lado da base (aresta) $a=12\text{ cm}$ e altura do prisma $h=15\text{ cm}$.
Calcule a área total e o volume.

A) Área total = $540+54\sqrt3\ \text{cm}^2$; Volume = $450\sqrt3\ \text{cm}^3$ B) Área total = $540+72\sqrt3\ \text{cm}^2$; Volume = $540\sqrt3\ \text{cm}^3$ C) Área total = $540+90\sqrt3\ \text{cm}^2$; Volume = $630\sqrt3\ \text{cm}^3$ D) Área total = $720+72\sqrt3\ \text{cm}^2$; Volume = $540\sqrt3\ \text{cm}^3$ E) Área total = $540+36\sqrt3\ \text{cm}^2$; Volume = $360\sqrt3\ \text{cm}^3$

Ver resposta (passo a passo)

$$\begin{aligned} p&=3a=3\cdot12=36\\ A_b&=\frac{\sqrt3}{4}a^2=\frac{\sqrt3}{4}\cdot144=36\sqrt3\\ A_L&=p\cdot h=36\cdot15=540\\[2mm] A_T&=A_L+2A_b=540+2\cdot36\sqrt3=\boxed{540+72\sqrt3\ \text{cm}^2}\\[2mm] V&=A_b\cdot h=36\sqrt3\cdot15=\boxed{540\sqrt3\ \text{cm}^3} \end{aligned}$$

Alternativa correta: B.

2) Base retângula — área total

Um prisma triangular tem base retângula com catetos $9$ cm e $12$ cm e altura do prisma $h=10$ cm.
Calcule a área total.

A) $456\ \text{cm}^2$ B) $468\ \text{cm}^2$ C) $486\ \text{cm}^2$ D) $432\ \text{cm}^2$ E) $492\ \text{cm}^2$

Ver resposta (passo a passo)

$$\begin{aligned} A_b&=\frac{b\cdot c}{2}=\frac{9\cdot12}{2}=54\\ \text{hip}&=\sqrt{9^2+12^2}=15\\ p&=9+12+15=36\\ A_L&=p\cdot h=36\cdot10=360\\ A_T&=A_L+2A_b=360+2\cdot54=\boxed{468\ \text{cm}^2} \end{aligned}$$

Alternativa correta: B.

3) Base escalena (Heron) — volume

Um prisma triangular tem base escalena de lados $8$, $11$ e $13$ cm e altura do prisma $h=18$ cm.
Calcule o volume.

A) $132\sqrt{30}\ \text{cm}^3$ B) $140\sqrt{30}\ \text{cm}^3$ C) $144\sqrt{30}\ \text{cm}^3$ D) $150\sqrt{30}\ \text{cm}^3$ E) $160\sqrt{30}\ \text{cm}^3$

Ver resposta (passo a passo)

$$\begin{aligned} s&=\frac{8+11+13}{2}=16\\ A_b&=\sqrt{s(s-a)(s-b)(s-c)}=\sqrt{16\cdot(16-8)\cdot(16-11)\cdot(16-13)}\\ &=\sqrt{16\cdot8\cdot5\cdot3}=\sqrt{1920}=8\sqrt{30}\\[2mm] V&=A_b\cdot h=8\sqrt{30}\cdot18=\boxed{144\sqrt{30}\ \text{cm}^3\ \approx\ 788{,}7\ \text{cm}^3} \end{aligned}$$

Alternativa correta: C.

Gabarito (alternativas)

1) B 2) B 3) C

8) Dicas rápidas

Tríade fixa: $A_L=p\,h$, $A_T=A_L+2A_b$, $V=A_b\,h$.
Base retângula: $A_b=\dfrac{b\,c}{2}$ e $p=b+c+\sqrt{b^2+c^2}$.
Equilátero: use as fórmulas do bloco “prisma triangular regular”.
Escaleno: Heron é a opção mais prática para $A_b$.

9) Veja também (links internos)

Área de Triângulo (todas as fórmulas) Triângulo Equilátero Triângulo Retângulo Isósceles Triângulos Semelhantes Poliedros Sólidos de Platão Fórmula de Euler Paralelepípedo Planificação do Paralelepípedo Planificação do Cubo Octaedro Esfera

10) Materiais recomendados

🧠 Mapas Mentais de Matemática 🎯 ENEM Matemática 📚 Coleção 10 eBooks 🗃️ Banco de Questões de Matemática 📺 Canais Oficiais de Matemática

Relacionadas

Fórmulas do Paralelepípedo

Prisma Pentagonal

Planificação do Cubo

"Artigo escrito por"

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.