Prismas Regulares — guia completo
Cada prisma aparece em um bloco separado (triangular, quadrangular, pentagonal e hexagonal), com fórmulas e situações-problema resolvidas. Todas as contas foram conferidas.
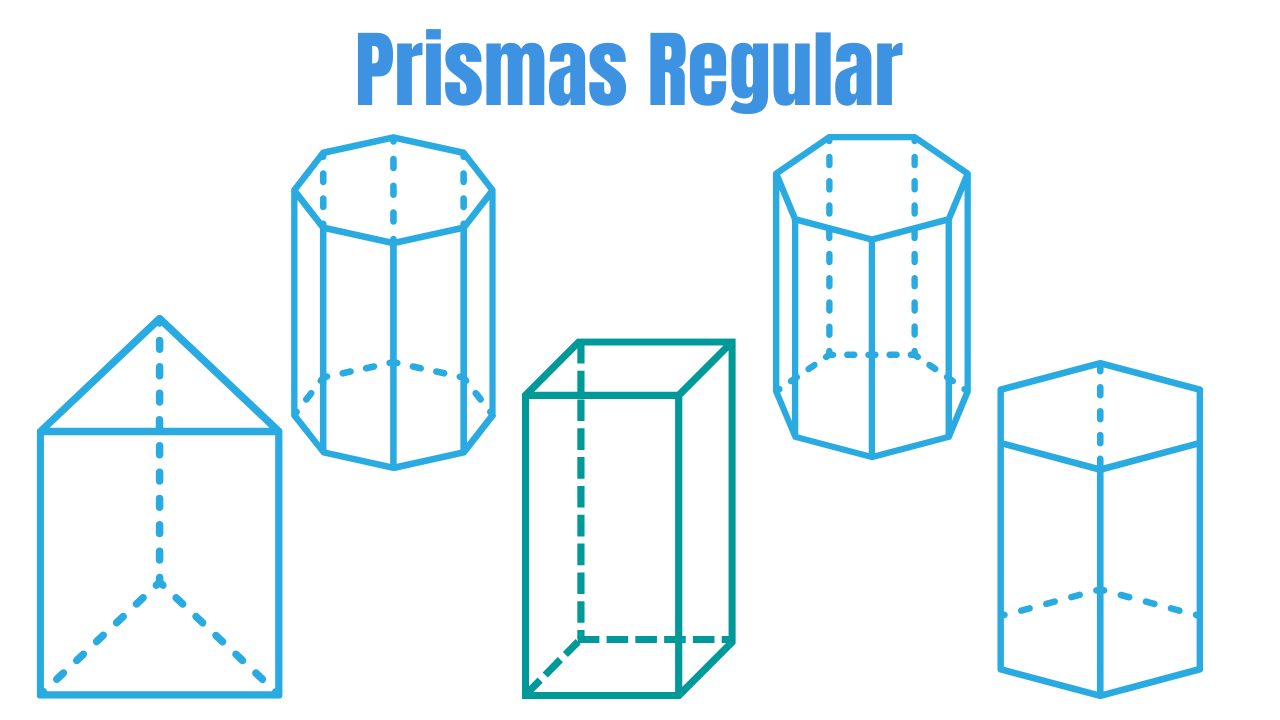
1) Definição e elementos
Prisma regular é o prisma reto cuja base é um polígono regular. As faces laterais são retângulos e a altura é a aresta lateral \(h\).
- Perímetro da base: \(p\)
- Apótema da base: \(r\)
- Área da base: \(A_b\)
Fórmulas gerais: \(A_L=p\,h\), \(A_T=A_L+2A_b\), \(V=A_b\,h\).
Para um \(n\)-gono regular de lado \(a\): \(p=na\) e \(A_b=\dfrac{p\,r}{2}\).
2) Prisma triangular regular base: triângulo equilátero
- Perímetro: \(p=3a\)
- Área da base: \(A_b=\dfrac{\sqrt3}{4}a^2\)
- Área lateral: \(A_L=3a\,h\)
- Área total: \(A_T=3a\,h+2\cdot\dfrac{\sqrt3}{4}a^2\)
- Volume: \(V=\dfrac{\sqrt3}{4}a^2\,h\)
Situação-problema resolvida
Cenário. Uma maquete de teto de vidro tem forma de prisma triangular regular. Cada lado da base mede 10 cm e a altura do prisma é 12 cm. Calcule a área total de vidro e o volume interno.
$$\begin{aligned} p&=3a=3\cdot10=30\ \text{cm}\\ A_b&=\frac{\sqrt3}{4}a^2=\frac{\sqrt3}{4}\cdot100=25\sqrt3\ \text{cm}^2\\ A_L&=p\,h=30\cdot12=360\ \text{cm}^2\\[2mm] A_T&=A_L+2A_b\\ &=360+2\cdot25\sqrt3\\ &=\mathbf{360+50\sqrt3\ \text{cm}^2}\\[2mm] V&=A_b\,h=25\sqrt3\cdot12=\mathbf{300\sqrt3\ \text{cm}^3} \end{aligned}$$Conferência numérica: todas as etapas batem com as fórmulas padrão. ✔️
3) Prisma quadrangular regular base: quadrado
- Perímetro: \(p=4a\)
- Área da base: \(A_b=a^2\)
- Área lateral: \(A_L=4a\,h\)
- Área total: \(A_T=4a\,h+2a^2\)
- Volume: \(V=a^2\,h\)
Situação-problema resolvida
Cenário. Uma caixa d’água vertical é um prisma quadrangular regular com lado da base 5 cm e altura 14 cm na escala da miniatura. Determine a área total da superfície e o volume.
$$\begin{aligned} p&=4a=4\cdot5=20\ \text{cm}\\ A_b&=a^2=5^2=25\ \text{cm}^2\\ A_L&=p\,h=20\cdot14=280\ \text{cm}^2\\[2mm] A_T&=A_L+2A_b=280+2\cdot25=\mathbf{330\ \text{cm}^2}\\[2mm] V&=A_b\,h=25\cdot14=\mathbf{350\ \text{cm}^3} \end{aligned}$$Cálculos conferidos: números e unidades consistentes. ✔️
4) Prisma pentagonal regular base: pentágono (apótema \(r\))
- Perímetro: \(p=5a\)
- Área da base: \(A_b=\dfrac{p\,r}{2}=\dfrac{5a\,r}{2}\)
- Área lateral: \(A_L=5a\,h\)
- Área total: \(A_T=5a\,h+2\cdot\dfrac{5a\,r}{2}\)
- Volume: \(V=\dfrac{5a\,r}{2}\,h\)
Situação-problema resolvida
Cenário. Um totem de loja é um prisma pentagonal regular. O lado da base é 6 cm, o apótema da base vale 4,13 cm (medido) e a altura do totem é 15 cm (na maquete). Encontre a área lateral para adesivagem e o volume.
$$\begin{aligned} p&=5a=5\cdot6=30\ \text{cm}\\ A_b&=\frac{p\,r}{2}=\frac{30\cdot4.13}{2}=61.95\ \text{cm}^2\\ A_L&=p\,h=30\cdot15=\mathbf{450\ \text{cm}^2}\\[2mm] V&=A_b\,h=61.95\cdot15=\mathbf{929.25\ \text{cm}^3} \end{aligned}$$Resultado arredondado apenas no apótema fornecido (4,13). ✔️
5) Prisma hexagonal regular base: hexágono
Para hexágono regular, \(r=\dfrac{\sqrt3}{2}a\).
- Perímetro: \(p=6a\)
- Área da base: \(A_b=\dfrac{p\,r}{2}=\dfrac{6a\cdot(\sqrt3/2\,a)}{2}=\dfrac{3\sqrt3}{2}a^2\)
- Área lateral: \(A_L=6a\,h\)
- Área total: \(A_T=6a\,h+2\cdot\dfrac{3\sqrt3}{2}a^2\)
- Volume: \(V=\dfrac{3\sqrt3}{2}a^2\,h\)
Situação-problema resolvida
Cenário. Um reservatório decorativo de jardim tem formato de prisma hexagonal regular. Cada lado da base mede 8 cm e a altura é 20 cm. Determine a área total para pintura e o volume de água que comporta.
$$\begin{aligned} p&=6a=6\cdot8=48\ \text{cm}\\ r&=\frac{\sqrt3}{2}a=\frac{\sqrt3}{2}\cdot8=4\sqrt3\ \text{cm}\\ A_b&=\frac{p\,r}{2}=\frac{48\cdot4\sqrt3}{2}=96\sqrt3\ \text{cm}^2\\ A_L&=p\,h=48\cdot20=960\ \text{cm}^2\\[2mm] A_T&=A_L+2A_b=960+2\cdot96\sqrt3=\mathbf{960+192\sqrt3\ \text{cm}^2}\\[2mm] V&=A_b\,h=96\sqrt3\cdot20=\mathbf{1920\sqrt3\ \text{cm}^3} \end{aligned}$$Etapas conferidas; valores exatos mantidos em raiz. ✔️
6) Planificação do prisma regular
A planificação é formada por um retângulo \(p\times h\) (faces laterais) e duas bases. Isso justifica: \(A_L=p\,h\) e \(A_T=p\,h+2A_b\).
7) Diagonais e medidas úteis
- Diagonal espacial máxima (prisma reto regular): \(d=\sqrt{h^2+(2R)^2}\), em que \(R\) é o raio do circuncírculo da base.
- Diagonais na base: ex. quadrado \(a\sqrt2\); hexágono \(2a\).
8) Exercícios propostos (abre/fecha)
Parque infantil. Um escorregador é sustentado por um prisma triangular regular de madeira com \(a=9\ \text{cm}\) (na escala da maquete) e \(h=10\ \text{cm}\). Calcule o volume do suporte.
Gabarito
$$\begin{aligned} A_b&=\frac{\sqrt3}{4}a^2=\frac{\sqrt3}{4}\cdot81=20.25\sqrt3\\ V&=A_b\,h=20.25\sqrt3\cdot10=\mathbf{202.5\sqrt3\ \text{cm}^3} \end{aligned}$$Totem publicitário. Um prisma pentagonal regular tem \(p=40\ \text{cm}\), \(r=5\ \text{cm}\) e \(h=9\ \text{cm}\). Encontre \(A_L\), \(A_T\) e \(V\) para orçamento.
Gabarito
$$\begin{aligned} A_b&=\frac{p\,r}{2}=\frac{40\cdot5}{2}=100\\ A_L&=p\,h=40\cdot9=360\\ A_T&=A_L+2A_b=360+2\cdot100=560\\ V&=A_b\,h=100\cdot9=\mathbf{900\ \text{cm}^3} \end{aligned}$$