9. Problemas de Contagem e Combinações
Os problemas de contagem e combinações fazem parte do raciocínio lógico e da análise combinatória, sendo muito frequentes em concursos. A solução desses problemas envolve a aplicação de princípios de contagem para determinar o número total de possibilidades em uma situação, utilizando métodos sistemáticos.
9.1 Princípio Fundamental da Contagem
O Princípio Fundamental da Contagem (ou Princípio Multiplicativo) é a base para resolver problemas de contagem simples. Ele afirma que:
Se um evento pode ocorrer de m maneiras e, após ele, outro evento pode ocorrer de n maneiras, então o total de maneiras em que ambos os eventos podem ocorrer é dado por:
Total = m×n
Exemplo 1:
Uma pessoa quer montar um prato escolhendo uma entrada e um prato principal. Se há 3 opções de entrada e 5 opções de prato principal, de quantas formas diferentes o prato pode ser montado?
Resolução:
- Entrada: 3 maneiras.
- Prato principal: 5 maneiras.
- Total: 3×5=15
👉Curso Gratuito de Raciocínio Lógico para Concursos
9.2 Princípio da Adição
O Princípio da Adição é aplicado quando temos eventos que não ocorrem simultaneamente (ou seja, são mutuamente exclusivos). Nesse caso, somamos o número de possibilidades de cada evento.
Exemplo 2:
Em uma cafeteria, há 4 opções de chá e 3 opções de suco. De quantas formas uma pessoa pode escolher um chá ou um suco?
Resolução:
- Chá: 4 maneiras.
- Suco: 3 maneiras.
- Total: 4+3 = 7 maneiras.
9.3 Permutações
Uma permutação ocorre quando os elementos de um conjunto são dispostos em ordem. O número total de permutações de nn elementos distintos é dado por:
P(n) = n!
onde n! (fatorial de n) é:
n! = n×(n−1)×(n−2)×⋯×1
Exemplo 3:
De quantas formas é possível organizar 3 livros em uma prateleira?
Resolução:
Temos 3 livros.
Número de permutações:
P(3) = 3! = 3×2×1 = 6
As possíveis ordens são:
ABC, ACB, BAC, BCA, CAB, CBA.
👉Entre no nosso canal do WhatsApp
9.4 Permutações com Repetição
Quando alguns elementos se repetem, a fórmula para permutações é:
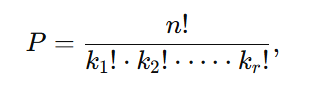
onde k1, k2, …, kr representam as quantidades de elementos repetidos.
Exemplo 4:
De quantas formas é possível organizar a palavra “ANA”?
Resolução:
Total de letras: 3!
A letra “A” se repete 2 vezes.
Fórmula:
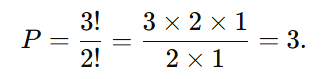
As permutações são: ANA, AAN, NAA.
9.5 Combinações
As combinações são usadas quando a ordem dos elementos não importa. A fórmula para calcular o número de combinações de nn elementos tomados k a k é:
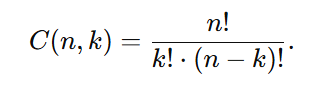
Exemplo 5:
Em um grupo de 5 pessoas, de quantas formas podemos escolher 2 pessoas para formar uma dupla?
Resolução:
Total de elementos: n = 5.
Elementos escolhidos: k = 2.
Fórmula:
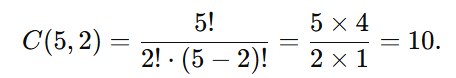
Total de combinações: 10.
9.6 Arranjos
Os arranjos são usados quando a ordem importa, mas os elementos escolhidos são apenas uma parte do conjunto total. A fórmula do arranjo de n elementos tomados k a k é:
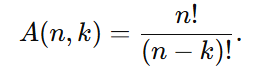
Exemplo 6:
De quantas formas é possível escolher 3 livros entre 5, colocando-os em ordem em uma prateleira?
Resolução:
Total de elementos: n = 5.
Elementos escolhidos: k = 3.
Fórmula:
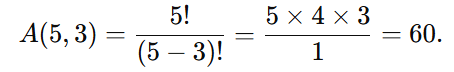
Total de arranjos: 60.
9.7 Exercícios Práticos
Exemplo 1: Em um restaurante, o cardápio tem 4 opções de entrada, 3 opções de prato principal e 2 opções de sobremesa. De quantas formas um cliente pode montar seu prato escolhendo uma opção de cada?
Resolução:
- Entrada: 4 maneiras.
- Prato principal: 3 maneiras.
- Sobremesa: 2 maneiras.
- Total: 4×3×2 = 24
Exemplo 2: Quantas combinações de 3 pessoas podem ser formadas a partir de um grupo de 6 pessoas?
Resolução:
Total de pessoas: n = 6.
Pessoas escolhidas: k = 3.
Fórmula:
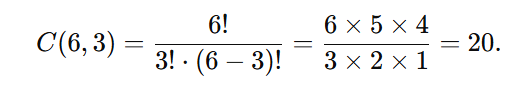
Total: 20 combinações.
Conclusão
Os problemas de contagem e combinações dentro da matemática exigem o uso sistemático do Princípio Fundamental da Contagem, permutação, combinação e arranjo. Saber identificar quando a ordem dos elementos importa ou não é crucial para resolver as questões corretamente. Praticar com exemplos variados é a chave para dominar esse conteúdo.
👉Curso Gratuito de Raciocínio Lógico para Concursos













