PROFMAT 2018 – Questão 03 | Geometria e Área de Triângulo
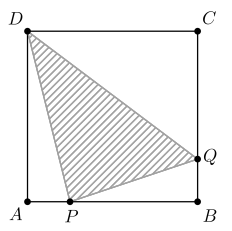
No quadrado ABCD abaixo, de lado 8, seja \( AP = BQ \). Qual o menor valor de \( AP \) para que a área do triângulo \( DPQ \) seja igual a \( 28 \)?
Ver solução passo a passo
Resposta correta: (C) \( 4 – 2\sqrt{2} \)
Chamando \( AP = BQ = x \), temos:
A área de \( DPQ \) pode ser calculada subtraindo a área do quadrado das áreas dos triângulos \( ADP \), \( BPQ \) e \( CDQ \).
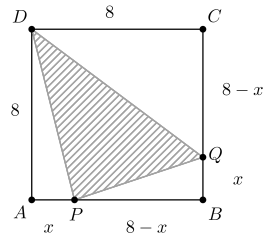
Área de \( DPQ \): \[ 64 – \frac{x \cdot (8-x)}{2} – \frac{x \cdot x}{2} – \frac{(8-x)\cdot x}{2} = 28 \]
Resolvendo a equação, obtemos o menor valor: \[ x = 4 – 2\sqrt{2}. \]
✅ Estude mais com nossos Mapas Mentais de Geometria
📘 Baixe também nossos 10 eBooks gratuitos e fortaleça seu aprendizado!
📚 Coleção A Matemática do Ensino Médio
Público-alvo: Professores de Matemática, Estudantes do PROFMAT, Amantes da Matemática, Alunos de Olimpíadas e Cursos de Licenciatura e Bacharelado.
📘 Questões PROFMAT de Anos Anteriores
📊 Estude Probabilidade
Aprenda definições, fórmulas e exercícios resolvidos de Probabilidade. Conteúdo direto, ideal para ENEM, vestibulares e concursos.
👉 Acessar o artigo de Probabilidade
