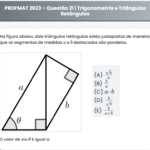
PROFMAT 2018 – Questão 04 | Comprimentos em malha quadriculada
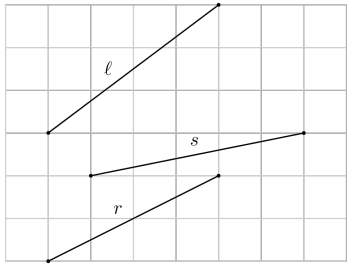
Na figura abaixo temos três segmentos dispostos em uma malha formada por quadrados congruentes. Sobre os comprimentos \( \ell, r, s \) dos três segmentos é correto afirmar que:
Ver solução passo a passo
Resposta correta: (D) \( r < \ell < s \)
Os três segmentos são hipotenusas de triângulos retângulos cujos vértices estão na malha.
- \( \ell = \sqrt{3^2 + 4^2} = \sqrt{25} = 5 \)
- \( s = \sqrt{1^2 + 5^2} = \sqrt{26} \approx 5,099 \)
- \( r = \sqrt{2^2 + 4^2} = \sqrt{20} \approx 4,472 \)
Logo, \( r < \ell < s \).
✅ Confira outros exercícios de Geometria Analítica e Trigonometria
📘 Baixe também nossos 10 eBooks gratuitos para reforço completo.
