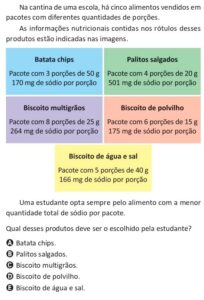
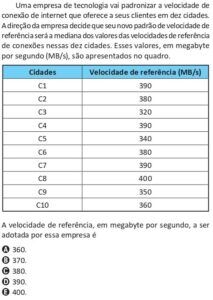
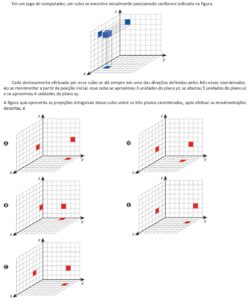
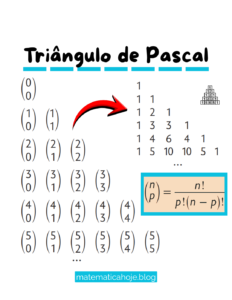
I. O triângulo de lados 4, 8 e 9 é acutângulo
PORQUE
II. \(4^2 + 8^2 < 9^2\).
A respeito dessas asserções, assinale a alternativa correta.
(A) As asserções I e II são proposições verdadeiras, e a II é uma justificativa correta da I.
(B) As asserções I e II são proposições verdadeiras, mas a II não é uma justificativa correta da I.
(C) A asserção I é uma proposição verdadeira, e a II é uma proposição falsa.
(D) A asserção I é uma proposição falsa, e a II é uma proposição verdadeira.
(E) As asserções I e II são proposições falsas.
Solução passo a passo:
No triângulo, o maior lado é oposto ao maior ângulo. Seja \(a = 9\), \(b = 8\) e \(c = 4\). O maior ângulo é \(\hat{A}\), oposto ao lado de comprimento 9.
Pela Lei dos Cossenos:
\[ \cos\hat{A} = \frac{b^2 + c^2 – a^2}{2bc} = \frac{8^2 + 4^2 – 9^2}{2 \cdot 8 \cdot 4} = \frac{64 + 16 – 81}{64} = -\frac{1}{64} < 0 \]
Como \(\cos\hat{A} < 0\), o ângulo \(\hat{A}\) é obtuso e o triângulo é obtusângulo. Portanto, a asserção I é falsa.
A asserção II é claramente verdadeira, pois:
\[ 4^2 + 8^2 = 16 + 64 = 80 < 81 = 9^2 \]
Logo, Resposta: (D) A I é falsa e a II é verdadeira.
🔹 Mapas Mentais de Matemática
🔹 Baixe os 10 eBooks de Matemática
📚 Coleção A Matemática do Ensino Médio
Público-alvo: Professores de Matemática, Estudantes do PROFMAT, Amantes da Matemática, Alunos de Olimpíadas e Cursos de Licenciatura e Bacharelado.
📘 Questões PROFMAT de Anos Anteriores
📊 Estude Probabilidade
Aprenda definições, fórmulas e exercícios resolvidos de Probabilidade. Conteúdo direto, ideal para ENEM, vestibulares e concursos.
👉 Acessar o artigo de Probabilidade