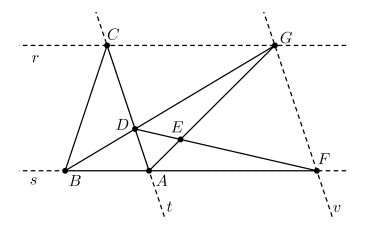
Na figura abaixo, \(r\) é paralela a \(s\), \(t\) é paralela a \(p\),
\(D\) é a interseção de \(BG\) com \(AC\) e \(E\) é a interseção de \(DF\) com \(AG\).
Se as áreas dos triângulos \(ADE\) e \(BCD\) são, respectivamente, 1 e 3,
a área do triângulo \(AEF\) é igual a
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Solução passo a passo:
Como as retas \(r\) e \(s\) são paralelas, os triângulos \(ABC\) e \(ABD\) possuem a mesma altura relativa à base \(AB\). Sendo \(AB\) a mesma base, temos:
\[ \text{área}(ABC) = \text{área}(ABD) + \text{área}(ADC) \]
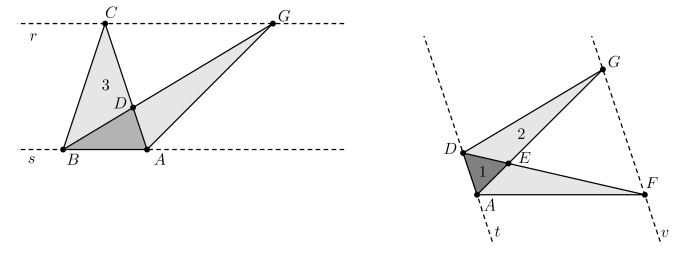
Sabendo que \(\text{área}(BCD) = 3\) e \(\text{área}(ADE) = 1\), analisando a figura temos:
\[ 3 = 1 + \text{área}(DEC) \quad \Rightarrow \quad \text{área}(DEC) = 2 \]
O triângulo \(ADF\) é semelhante a \(ADC\), e as áreas correspondentes se relacionam proporcionalmente. Assim, somando as áreas:
\[ \text{área}(ADE) + \text{área}(DEC) + \text{área}(AEF) = 1 + 2 + \text{área}(AEF) \]
Logo:
\[ \text{área}(AEF) = 2 \]
Resposta: (B) 2
🔹 Mapas Mentais de Matemática
🔹 Baixe os 10 eBooks de Matemática
📚 Coleção A Matemática do Ensino Médio
Público-alvo: Professores de Matemática, Estudantes do PROFMAT, Amantes da Matemática, Alunos de Olimpíadas e Cursos de Licenciatura e Bacharelado.
📘 Questões PROFMAT de Anos Anteriores
📊 Estude Probabilidade
Aprenda definições, fórmulas e exercícios resolvidos de Probabilidade. Conteúdo direto, ideal para ENEM, vestibulares e concursos.
👉 Acessar o artigo de Probabilidade




























