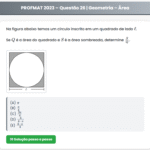
Sabendo que
\[
\begin{cases}
1 + \cos x = a \cdot sen x \\
1 – \cos x = b \cdot sen x
\end{cases}
\]
onde \(a\) e \(b\) são números reais e \(0 < x < \frac{\pi}{2}\), podemos afirmar que:
(A) \(a+b=2\)
(B) \(a+b=-2\)
(C) \(a^2+b^2=2\)
(D) \(a^2-b^2=0\)
(E) \(a\cdot b=1\)
Solução passo a passo:
Como \(0 < x < \frac{\pi}{2}\), temos \(sen x \neq 0\), então:
\[ a = \frac{1+\cos x}{sen x}, \quad b = \frac{1-\cos x}{sen x} \]
Logo, o produto \(a \cdot b\) será:
\[ a \cdot b = \frac{1+\cos x}{sen x} \cdot \frac{1-\cos x}{sen x} = \frac{1-\cos^2 x}{sen^2 x} = \frac{sen^2 x}{sen^2 x} = 1 \]
Resposta: (E) \(a \cdot b = 1\)
🔹 Mapas Mentais de Matemática
🔹 Baixe os 10 eBooks de Matemática
📚 Coleção A Matemática do Ensino Médio
Público-alvo: Professores de Matemática, Estudantes do PROFMAT, Amantes da Matemática, Alunos de Olimpíadas e Cursos de Licenciatura e Bacharelado.
📘 Questões PROFMAT de Anos Anteriores
📊 Estude Probabilidade
Aprenda definições, fórmulas e exercícios resolvidos de Probabilidade. Conteúdo direto, ideal para ENEM, vestibulares e concursos.
👉 Acessar o artigo de Probabilidade