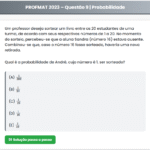
Uma prova pode ter dois tipos de questão: objetivas e discursivas. A primeira prova possuía 35 questões objetivas, 3 discursivas e duração de 4 horas. A segunda prova possuía 30 questões objetivas e 3 horas de duração.
Sabendo que o tempo máximo gasto em cada tipo de questão é constante em todas as provas, se fosse formulada uma terceira prova com 30 questões objetivas e duração de 4 horas, com o mesmo padrão das anteriores, esta prova poderia ter, no máximo, quantas questões discursivas?
(A) 4
(B) 5
(C) 6
(D) 8
(E) 10
Ver solução passo a passo
Resposta correta: (C)
Na segunda prova, 30 questões objetivas devem ser resolvidas em 3 horas (180 minutos). Assim, cada questão objetiva leva:
\[ \frac{180}{30} = 6 \text{ minutos por questão.} \]
Na primeira prova, com 35 questões objetivas, o tempo gasto nelas é:
\[ 35 \times 6 = 210 \text{ minutos.} \]
O tempo total da prova é de 240 minutos, então sobram \(240 – 210 = 30\) minutos para as 3 questões discursivas, ou seja:
\[ \frac{30}{3} = 10 \text{ minutos por questão discursiva.} \]
Na terceira prova, com 30 questões objetivas e 4 horas de duração, restará 1 hora (60 minutos) para questões discursivas. Cada uma leva 10 minutos, então teremos:
\[ \frac{60}{10} = 6 \text{ questões discursivas.} \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!