A base (lado distinto) de um triângulo isósceles mede \(6 \, \text{cm}\) e a altura relativa a esta base mede \(4 \, \text{cm}\). Nele inscrevemos outro triângulo isósceles, com base paralela à base do triângulo original e vértice oposto no ponto médio da base do triângulo original, de modo que a área do triângulo inscrito seja a maior possível. A área, em \(cm^2\), do triângulo inscrito é:
(A) \( \frac{1}{2} \)
(B) 2
(C) 3
(D) 4
(E) 6
Ver solução passo a passo
Resposta correta: (C)
Seja \(ABC\) o triângulo isósceles de base \(6\) e altura \(4\). Inscrevemos o triângulo \(MPQ\) com base \(PQ \parallel AB\) e vértice \(M\) no ponto médio de \(AB\), conforme a figura.
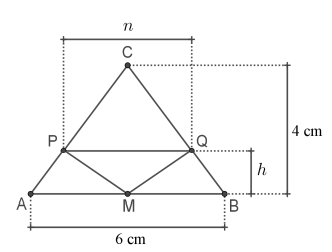
Seja \(PQ = n\) e \(h\) a altura do triângulo \(MPQ\). Pela semelhança de triângulos:
\[ \frac{n}{6} = \frac{4-h}{4} \quad \Rightarrow \quad n = 12 – 3h \]
Área do triângulo inscrito: \[ S = \frac{n \cdot h}{2} = \frac{(12-3h)\cdot h}{2} = 6h – \frac{3h^2}{2} \]
A área \(S(h)\) é uma função quadrática do tipo \(S = -\frac{3}{2}h^2 + 6h\). O vértice fornece a área máxima:
\[ h_\text{máx} = -\frac{b}{2a} = -\frac{6}{2 \cdot -\frac{3}{2}} = 2 \]
Substituindo \(h = 2\): \[ S_\text{máx} = 6\cdot 2 – \frac{3\cdot 2^2}{2} = 12 – 6 = 6 \]
Área do triângulo inscrito: \[ 3 \, \text{cm}^2 \]

📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!