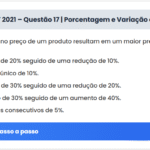
Na figura, \( AB = AC = 7 \), \( CB = 2 \), \( BD = 10 \) e \( BE \) é bissetriz do ângulo \( DBA \). Nessas condições, \( AE \) é igual a:
Ver solução passo a passo
Resposta correta: (B)
O triângulo \( BAC \) é isósceles de vértice \( A \) e \( CB = 2 \). Se \( AH \) é a altura relativa a \( BC \), então \( HB = 1 \).
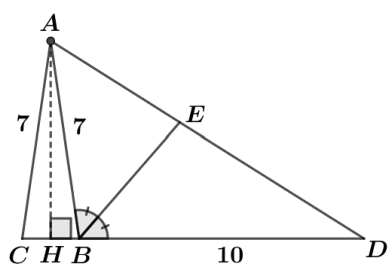
Considerando o triângulo retângulo \( AHB \):
\[ AB^2 = AH^2 + HB^2 \quad \Rightarrow \quad 7^2 = AH^2 + 1^2 \] \[ AH = \sqrt{49 – 1} = \sqrt{48} \]
Agora, considerando o triângulo retângulo \( AHD \):
\[ AD^2 = AH^2 + HD^2 \] \[ AD^2 = 48 + 121 = 169 \quad \Rightarrow \quad AD = 13 \]
Pelo **Teorema das Bissetrizes Internas** no triângulo \( ABD \):
\[ \frac{AE}{AB} = \frac{AD}{AB + BD} \]
\[ \frac{AE}{7} = \frac{13}{17} \quad \Rightarrow \quad AE = \frac{91}{17} \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!
