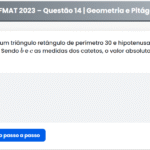
Sobre os catetos de um triângulo retângulo cujo maior ângulo agudo mede \( \alpha \) são construídos hexágonos regulares e sobre a hipotenusa um triângulo equilátero, conforme indicado na figura. Se \( \tan \alpha = 2 \) e a área do hexágono menor mede 1, então as áreas do triângulo equilátero e do hexágono maior medem, respectivamente:
(A) \( \frac{5}{6} \text{ e } 4 \)
(B) \( \frac{1}{2} \text{ e } 2 \)
(C) \( \frac{4\sqrt{3}}{9} \text{ e } 2 \)
(D) \( \frac{5}{3} \text{ e } 4 \)
(E) \( \frac{4\sqrt{3}}{9} \text{ e } 6 \)
Ver solução passo a passo
Resposta correta: (A)
Como os hexágonos são regulares e semelhantes, a razão de semelhança entre seus lados é igual à razão entre os catetos do triângulo retângulo. Como \( \tan \alpha = 2 \), a razão de semelhança é 2, logo a razão entre as áreas é:
\[ 2^2 = 4 \]
Portanto, se a área do hexágono menor é 1, a do hexágono maior será 4.
Agora, para o hexágono construído sobre a hipotenusa, sua área será a soma das áreas dos hexágonos sobre os catetos: \[ 1 + 4 = 5 \]
Esse hexágono é formado por 6 triângulos equiláteros iguais, então a área de cada triângulo equilátero é:
\[ \frac{5}{6} \]
Logo, as áreas pedidas são:
\[ \frac{5}{6} \text{ e } 4 \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!