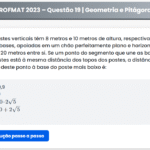
Quando aberta, uma torneira A é capaz de encher completamente um tanque em 10 horas, mantendo vazão constante. Uma torneira B esvazia o tanque com uma vazão constante ainda desconhecida.
Com o tanque vazio, abriu-se a torneira A. Duas horas depois, abriu-se também a torneira B. Três horas depois de ambas abertas, o tanque estava novamente vazio.
Em quanto tempo a torneira B conseguiria esvaziar totalmente o tanque, caso ele estivesse completamente cheio e a torneira A permanecesse fechada?
(A) 2 horas
(B) 3 horas
(C) 4 horas
(D) 5 horas
(E) 6 horas
Ver solução passo a passo
Resposta correta: (E)
1. **Vazão da torneira A**: A torneira A enche o tanque em 10 horas, então sua vazão é: \[ \frac{1}{10} \text{ do tanque por hora.} \]
2. **Volume após 2 horas apenas com A aberta**: \[ 2 \times \frac{1}{10} = \frac{2}{10} = \frac{1}{5} \]
3. **Esvaziamento em 3 horas com as duas torneiras**: Os \( \frac{1}{5} \) do tanque são esvaziados em 3 horas, ou seja, em cada hora esvaziamos: \[ \frac{1}{5} \div 3 = \frac{1}{15} \]
Como A continua enchendo com \( \frac{1}{10} \) por hora, a vazão de B deve ser: \[ b – \frac{1}{10} = \frac{1}{15} \quad \Rightarrow \quad b = \frac{1}{6} \]
4. **Tempo para esvaziar o tanque apenas com B aberta**: \[ 1 \div \frac{1}{6} = 6 \text{ horas.} \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!