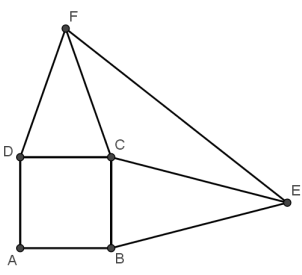
Na figura abaixo, \(ABCD\) é um quadrado de lado \(2\), \(BE = CE = 4\) e \(DF = CF = 3\). A medida do segmento \(EF\) é:
(A) \( 5 \)
(B) \( \sqrt{25} \)
(C) \( \sqrt{31 + 4\sqrt{8} + 4\sqrt{15}} \)
(D) \( \sqrt{25 + 2\sqrt{8} + 2\sqrt{15}} \)
(E) \( \sqrt{25 + 2\sqrt{8} + 2\sqrt{15}} \)
Ver solução passo a passo
Resposta correta: (E)
Sejam \(G\) o centro do quadrado, \(H\) o ponto médio de \(BC\) e \(I\) o ponto médio de \(CD\).
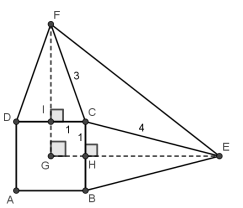
1. **Cálculo da altura em \( \triangle BEC \)** O triângulo \(BEC\) é isósceles com \(BE = CE = 4\) e base \(BC = 2\). Pela altura \(EH\): \[ EH = \sqrt{4^2 – 1^2} = \sqrt{15} \] Logo, \(FI = \sqrt{8}\) de forma análoga.
2. **Cálculo das distâncias para o teorema de Pitágoras em \( \triangle EGF \)** Como \(GI = GH = 1\), temos: \[ GE = 1 + \sqrt{15}, \quad GF = 1 + \sqrt{8} \]
3. **Cálculo de \(EF\)** Pelo Teorema de Pitágoras na diagonal \(EF\): \[ EF^2 = (1 + \sqrt{8})^2 + (1 + \sqrt{15})^2 \] \[ EF^2 = 1 + 2\sqrt{8} + 8 + 1 + 2\sqrt{15} + 15 \] \[ EF^2 = 25 + 2\sqrt{8} + 2\sqrt{15} \] \[ EF = \sqrt{25 + 2\sqrt{8} + 2\sqrt{15}} \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!





























