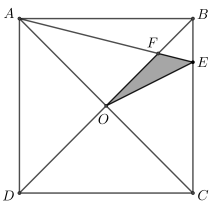
\(ABCD\) é um quadrado de lado \(4\). Sabendo que \(BE = 1\), \(O\) é o centro do quadrado, \(F\) é a interseção de \(OB\) com \(AE\), a área do triângulo \(OFE\) é igual a:
(A) \( \frac{1}{5} \)
(B) \( \frac{2}{5} \)
(C) \( \frac{3}{5} \)
(D) \( \frac{1}{4} \)
(E) \( \frac{3}{4} \)
Ver solução passo a passo
Resposta correta: (C)
1. **Semelhança de triângulos** Pela semelhança entre \( \triangle AFD \) e \( \triangle BFE \), temos: \[ BF = \frac{DF}{4} \] E como \(DO = OB = OF + BF\), encontramos: \[ DF = BF + 2 \cdot OF \] \[ BF = \frac{BF + 2 \cdot OF}{4} \quad \Rightarrow \quad BF = \frac{2 \cdot OF}{3} \]
2. **Relação entre áreas** Seja \(S_1\) a área de \( \triangle OFE \) e \(S_2\) a área de \( \triangle BFE \). Sabemos que \(S_1 + S_2 = 1\) e \(\frac{S_1}{S_2} = \frac{3}{2}\). Resolvendo o sistema: \[ S_1 = \frac{3}{5} \]
Portanto, a área de \( \triangle OFE \) é:
\[ \frac{3}{5} \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!
































