Na figura abaixo, temos um quadrado \(ABCD\) e um triângulo equilátero \(ABE\).
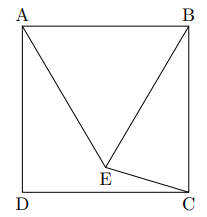
Indicando por \(\alpha\) o ângulo \( \widehat{ECD} \), podemos afirmar que \( \tan \alpha \) é igual a:
(A) \( \frac{2 – \sqrt{3}}{2} \)
(B) \( \frac{2 + \sqrt{3}}{2} \)
(C) \( \frac{2 – \sqrt{3}}{2 + \sqrt{3}} \)
(D) \( 2 + \sqrt{3} \)
(E) \( 2 – \sqrt{3} \)
Ver solução passo a passo
Resposta correta: (E)
Chamemos a medida do lado do quadrado de \( \ell \). Seja \( FG \) o segmento paralelo a \( AD \) passando por \( E \), conforme a figura.
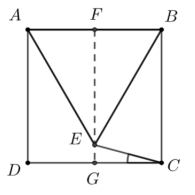
Assim:
\[ FG = \ell, \quad FE = \frac{\ell \sqrt{3}}{2} \] pois é a altura do triângulo equilátero de lado \( \ell \).
A tangente do ângulo \(\alpha\) pode ser calculada por: \[ \tan \alpha = \frac{EG}{GC} \] Como \( EG = FG – EF \), temos: \[ EG = \ell – \frac{\ell \sqrt{3}}{2}, \quad GC = \frac{\ell}{2} \] Logo: \[ \tan \alpha = \frac{\ell – \ell \sqrt{3}/2}{\ell / 2} = \frac{2\ell – \ell \sqrt{3}}{\ell} = 2 – \sqrt{3} \]
📘 E baixe os 10 eBooks de Matemática para turbinar seus estudos!