PROFMAT 2023 – Questão 21 | Trigonometria e Triângulos Retângulos
Na figura abaixo, dois triângulos retângulos estão justapostos de maneira que os segmentos de medidas \(a\) e \(b\) destacados são paralelos.
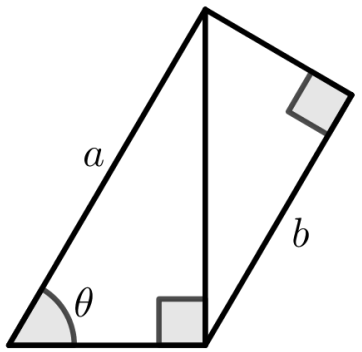
O valor de \(\sin \theta\) é igual a:
(A) \( \frac{\sqrt{b}}{a} \)
(B) \( \frac{b}{a} \)
(C) \( a – b \)
(D) \( \frac{b}{\sqrt{a}} \)
(E) \( \frac{b}{a+b} \)
(B) \( \frac{b}{a} \)
(C) \( a – b \)
(D) \( \frac{b}{\sqrt{a}} \)
(E) \( \frac{b}{a+b} \)
Resposta correta: (A) \( \frac{\sqrt{b}}{a} \)
Pelo enunciado, temos dois triângulos retângulos semelhantes, com lados \(a\) e \(b\) paralelos.
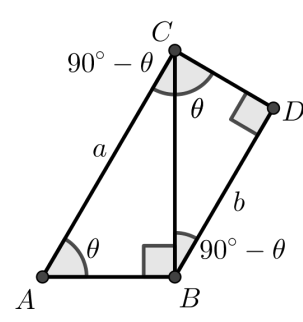
Considerando os ângulos e aplicando a definição de seno no triângulo maior: \[ \sin \theta = \frac{BC}{AB} = \frac{\sqrt{b}}{a}. \]
Portanto, concluímos que: \[ \boxed{\sin \theta = \frac{\sqrt{b}}{a}} \]
🔗 Continue seus estudos:
































