PROFMAT 2023 – Questão 26 | Geometria – Área
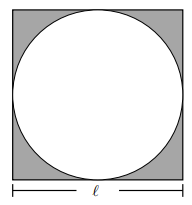
Na figura abaixo temos um círculo inscrito em um quadrado de lado \( \ell \).
Se \( Q \) é a área do quadrado e \( S \) é a área sombreada, determine \( \frac{S}{Q} \).
(A) \( \pi \)
(B) \( \frac{\pi}{4} \)
(C) \( \frac{3\pi}{4} \)
(D) \( \frac{4}{4-\pi} \)
(E) \( \frac{4-\pi}{4} \)
(B) \( \frac{\pi}{4} \)
(C) \( \frac{3\pi}{4} \)
(D) \( \frac{4}{4-\pi} \)
(E) \( \frac{4-\pi}{4} \)
Resposta correta: (E) \( \frac{4-\pi}{4} \)
A área do quadrado é \( Q = \ell^2 \).
A área do círculo inscrito é \( \pi \left(\frac{\ell}{2}\right)^2 = \frac{\pi \ell^2}{4} \).
A área sombreada é: \[ S = \ell^2 – \frac{\pi \ell^2}{4} = \ell^2 \left(1 – \frac{\pi}{4}\right) \]
Logo, a razão é: \[ \frac{S}{Q} = 1 – \frac{\pi}{4} = \frac{4 – \pi}{4} \]
🔗 Continue seus estudos:





























