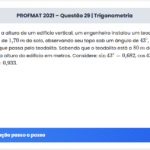
Considere um ângulo agudo \( \alpha \) tal que \( sen \alpha + \cos \alpha = \frac{7}{5} \). Neste caso, tem-se que \( |sen \alpha – \cos \alpha| \) é igual a:
(B) \( \frac{4}{5} \)
(C) \( \frac{3}{5} \)
(D) \( \frac{2}{5} \)
(E) \( \frac{1}{5} \)
Resposta correta: (E) \( \frac{1}{5} \).
Usando a identidade: \[ (sen \alpha + \cos \alpha)^2 = sen^2 \alpha + \cos^2 \alpha + 2 sen \alpha \cos \alpha \] Temos: \[ \left(\frac{7}{5}\right)^2 = 1 + 2 sen \alpha \cos \alpha \quad \Rightarrow \quad \frac{49}{25} = 1 + 2 sen \alpha \cos \alpha \]
Portanto: \[ 2 sen \alpha \cos \alpha = \frac{24}{25} \]
Para calcular \( |sen \alpha – \cos \alpha| \), usamos: \[ (sen \alpha – \cos \alpha)^2 = 1 – 2 sen \alpha \cos \alpha \] \[ (sen \alpha – \cos \alpha)^2 = 1 – \frac{24}{25} = \frac{1}{25} \] \[ |sen \alpha – \cos \alpha| = \frac{1}{5} \]
🔗 Continue seus estudos com nossos recursos: