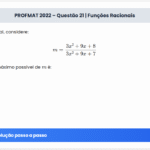
Com \( \ell \) metros de arame um fazendeiro precisa cercar uma área retangular. Sabendo que um dos lados do retângulo não terá cerca, pois ficará junto a um rio, qual é a maior área possível de ser cercada, em \( m^2 \)?
(B) \( \frac{\ell^2}{4} \)
(C) \( \frac{\ell^2}{6} \)
(D) \( \frac{\ell^2}{8} \)
(E) \( \frac{\ell^2}{10} \)
Resposta correta: (D) \( \frac{\ell^2}{8} \).
Seja \( x \) o lado perpendicular ao rio e \( y \) o lado paralelo ao rio. A quantidade de arame nos dá a equação: \[ 2x + y = \ell \quad \Rightarrow \quad y = \ell – 2x \]
A área do retângulo é: \[ A = x \cdot y = x(\ell – 2x) \] Para área máxima, derivamos ou completamos quadrado, obtendo: \[ x = \frac{\ell}{4}, \quad y = \frac{\ell}{2} \]
A área máxima será: \[ A_\text{máx} = x \cdot y = \frac{\ell}{4} \cdot \frac{\ell}{2} = \frac{\ell^2}{8} \]
🔗 Continue seus estudos com nossos recursos: