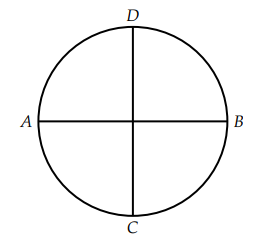
Uma empresa cobra por metro quadrado de forro de gesso. Quando precisa forrar uma superfície circular, o empreiteiro multiplica as medidas dos dois diâmetros do círculo para estimar a área (\(AB \times CD\), na figura). Essa estratégia superestima a área real, fazendo a empresa cobrar a mais.
Com um custo de R$50,00 por metro quadrado, qual das opções melhor se aproxima do valor cobrado a mais pela empresa para forrar uma superfície circular com raio de 2 metros?
(B) R$160,00
(C) R$140,00
(D) R$125,00
(E) R$100,00
Resposta correta: (A) R$172,00.
A área do círculo com raio \( r = 2 \) é: \[ A = \pi r^2 = 4\pi \] O custo correto seria: \[ 4\pi \cdot 50 \approx 628 \text{ reais.} \]
Usando a aproximação incorreta \( AB \times CD = 4 \times 4 = 16 \, m^2 \), o custo calculado seria: \[ 16 \cdot 50 = 800 \text{ reais.} \]
Portanto, o valor cobrado a mais será: \[ 800 – 628 \approx 172 \text{ reais.} \]
🔗 Continue seus estudos com nossos recursos:





























