Progressão Geométrica (PG)

Progressão Geométrica (PG) — Definição, Termo Geral, Somatórios, Classificação e Exercícios

Progressão Geométrica (PG) — Guia Completo

Definição, características, termo geral, soma finita, soma infinita e classificação (crescente, decrescente, alternante), com exemplos e exercícios de múltipla escolha. Para o caso aditivo, compare com a Progressão Aritmética (PA).

📘 Mapas Mentais 🎯 ENEM Matemática 📚 10 eBooks 🧩 Banco de Questões 📡 Canais Oficiais

Definição e Características

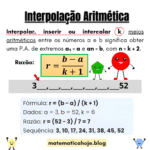
Uma Progressão Geométrica (PG) é uma sequência em que cada termo, a partir do segundo, é obtido multiplicando o anterior por uma constante chamada razão \((q)\).

\[ a_n = a_{n-1}\cdot q \quad (n\ge 2) \qquad\text{e}\qquad q=\frac{a_n}{a_{n-1}}\ (\text{com }a_{n-1}\ne 0). \]
  • Primeiro termo: \(a_1\)
  • Razão: \(q\) (fator multiplicativo constante)
  • Exemplos: \(3, 6, 12, 24,\dots\) (\(q=2\)); \(81, 27, 9, 3,\dots\) (\(q=\tfrac13\)); \(2,-6,18,-54,\dots\) (\(q=-3\)).

Exercícios do tópico

Ex. 1 — Identifique \(q\). Sequência: \(5,\ 10,\ 20,\ 40,\dots\). Qual é a razão?

Ver solução
\(\displaystyle q=\frac{10}{5}=2\) (verificando: \(20/10=2\), \(40/20=2\)).

Ex. 2 — É PG? Sequência: \(9,\ 6,\ 4,\ \tfrac{8}{3},\dots\). As razões sucessivas são constantes?

Ver solução
\(6/9=2/3,\ 4/6=2/3,\ (8/3)/4=2/3\Rightarrow\) sim, PG com \(q=\tfrac23\).

Termo Geral da PG

Para \(n\ge 1\), o \(n\)-ésimo termo de uma PG é dado por:

\[ \boxed{a_n = a_1\cdot q^{\,n-1}} \]
Exemplo: Em \(2,\ 6,\ 18,\ 54,\dots\) (\(a_1=2,\ q=3\)), \(a_{8}=2\cdot 3^{7}=4374\).

Exercícios do tópico

Ex. 1 — Calcule \(a_{12}\). \(a_1=5,\ q=2\).

Ver solução
\(a_{12}=5\cdot 2^{11}=5\cdot 2048=10240.\)

Ex. 2 — Encontre \(a_1\). Numa PG, \(a_6=81\) e \(q=3\). Determine \(a_1\).

Ver solução
\(a_6=a_1\cdot 3^{5}\Rightarrow a_1=\frac{81}{243}=\tfrac{1}{3}.\)

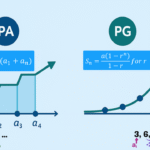
Soma dos n Primeiros Termos da PG

Se \(q\ne 1\), a soma \(S_n\) dos \(n\) primeiros termos é:

\[ \boxed{S_n=a_1\,\frac{q^n-1}{q-1}} \qquad\text{ou}\qquad \boxed{S_n=a_1\,\frac{1-q^n}{1-q}} \]

Para \(q=1\), a PG é constante e \(S_n=n\cdot a_1\).

Exemplo: PG de razão \(q=2\) com \(a_1=3\). \(S_6=3\cdot\frac{2^6-1}{2-1}=3(64-1)=189\).

Exercícios do tópico

Ex. 1 — Calcule \(S_{10}\). \(a_1=2,\ q=3\).

Ver solução
\(S_{10}=2\cdot\frac{3^{10}-1}{3-1}=2\cdot\frac{59049-1}{2}=59048.\)

Ex. 2 — PG constante. \(a_1=7,\ q=1\). Encontre \(S_{15}\).

Ver solução
\(S_{15}=15\cdot 7=105.\)

Soma Infinita de uma PG

Uma PG infinita converge (tem soma finita) somente quando o módulo da razão é menor que 1: \(|q|<1\).

\[ \text{Se }|q|<1,\quad \boxed{S_{\infty}=\frac{a_1}{1-q}}. \]
Exemplo: \(a_1=5\) e \(q=\tfrac12\). \(S_{\infty}=\dfrac{5}{1-\tfrac12}=10\).

Exercícios do tópico

Ex. 1 — Convergência. \(a_1=12\) e \(q=0{,}8\). Calcule \(S_\infty\).

Ver solução
\(|q|=0{,}8<1\Rightarrow S_\infty=\dfrac{12}{1-0{,}8}=60.\)

Ex. 2 — Divergência. \(a_1=4\) e \(q=-\tfrac{3}{2}\). Existe \(S_\infty\)?

Ver solução
\(|q|=1{,}5>1\Rightarrow\) a série diverge; não há soma infinita.

Classificação da PG

O comportamento de uma PG depende de \(a_1\) e, principalmente, da razão \(q\):

  • Crescente: \(a_1>0\) e \(q>1\); ou \(a_1<0\) e \(0<q<1\) (em valor absoluto, os termos aproximam-se de 0 mas “sobem” no eixo negativo).
  • Decrescente: \(a_1>0\) e \(0<q<1\); ou \(a_1<0\) e \(q>1\).
  • Alternante: \(q<0\). Os termos alternam de sinal; o módulo pode crescer (\(|q|>1\)) ou decrescer (\(|q|<1\)).
Exemplos rápidos:
  • \(a_1=3,\ q=2\) ⇒ \(3,6,12,\dots\) (crescente).
  • \(a_1=9,\ q=\tfrac13\) ⇒ \(9,3,1,\tfrac13,\dots\) (decrescente, converge para 0).
  • \(a_1=2,\ q=-\tfrac12\) ⇒ \(2,-1,0{,}5,-0{,}25,\dots\) (alternante, \(|q|<1\), converge para 0).

Exercícios de PG — Múltipla Escolha (progressão de dificuldade)

Clique numa alternativa para ver a correção e abrir a solução detalhada.

1) A sequência \(3,\,6,\,12,\,24,\dots\) é uma PG. A razão \(q\) é:
Ver solução
\(q=6/3=2\). Próximos termos: \(48,\,96\).
2) Numa PG com \(a_1=5\) e \(q=3\), o termo \(a_8\) vale:
Ver solução
\(a_8=5\cdot3^{7}=5\cdot2187=10\,935\).
3) Para \(a_1=2\) e \(q=2\), a soma \(S_{10}\) é:
Ver solução
\(S_{10}=2\cdot\frac{2^{10}-1}{2-1}=2(1024-1)=2046\).
4) Em \(a_1=81\) e \(q=\tfrac13\), o par correto \((a_{10},\,S_{10})\) é:
Ver solução
\(a_{10}=81\cdot(1/3)^9=1/243\). \(S_{10}=81\cdot\frac{1-(1/3)^{10}}{1-1/3}=\frac{29524}{243}\approx 121{,}50\).
5) Em \(a_n=4\cdot3^{\,n-1}\), o menor \(n\) com \(a_n>10\,000\) é:
Ver solução
\(3^{n-1}>2500\). Como \(3^7=2187\) e \(3^8=6561\), precisa \(n-1\ge 8\Rightarrow n=9\).
6) Para \(a_1=1,\ q=2\), qual \(n\) satisfaz \(S_n=2047\)?
Ver solução
\(S_n=2^{n}-1=2047\Rightarrow 2^n=2048=2^{11}\Rightarrow n=11\).
7) Capital \(R\$\,1000{,}00\) a \(5\%\)/mês. Valor no \(12^\circ\) mês (padrão \(a_n=a_1q^{n-1}\)) é aproximadamente:
Ver solução
\(a_{12}=1000\cdot1{,}05^{11}\approx 1\,710{,}34\). (*Se considerar 12 capitalizações completas: \(1\,795{,}86\).* )
8) Bem de R$ 50.000 com depreciação de \(20\%\)/ano. Valor após 5 anos:
Ver solução
\(V_5=50\,000\cdot 0{,}8^{5}=50\,000\cdot0{,}32768=16\,384{,}00\).
9) Para \(a_1=12\) e \(q=-\tfrac13\), o par \((a_5,\,S_\infty)\) correto é:
Ver solução
\(a_5=12(-\tfrac13)^4=\tfrac{4}{27}\). Como \(|q|<1\), \(S_\infty=\dfrac{12}{1-(-1/3)}=9\).
10) Três meios geométricos entre 2 e 162 são:
Ver solução
\(2\cdot q^4=162\Rightarrow q=3\). Meios: \(6,18,54\).
11) Sabendo \(a_3=48\) e \(a_7=3072\), admitindo \(q>0\), temos:
Ver solução
\(\frac{a_7}{a_3}=q^4=64\Rightarrow q=2\) (com \(q>0\)). \(a_3=a_1q^2\Rightarrow a_1=48/4=12\).
12) Em \(|q|<1\) com \(S_\infty=20\) e \(a_4=1{,}25\), os valores corretos são:
Ver solução
\(a_1=20(1-q)\) e \(a_4=a_1q^3=1{,}25\). Uma solução com \(|q|<1\): \(q=1/2,\ a_1=10\).
Gabarito: 1)A 2)C 3)A 4)B 5)B 6)B 7)B 8)B 9)A 10)B 11)A 12)A

Materiais recomendados

Aprenda PG e PA com materiais práticos do blog:

📘 Mapas Mentais de Matemática 🎯 Guia ENEM Matemática 📚 Coleção 10 eBooks 🧩 Banco de Questões 📡 Canais Oficiais ➕ Estudar PA agora
Relacionadas

Sequências Especiais 

Definição de Progressão Aritmética (P.A.)

Soma dos Termos de P.G. Finita

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube