Propriedades da Função Exponencial
Descubra as principais propriedades da função exponencial, exemplos resolvidos e exercícios de múltipla escolha para praticar.
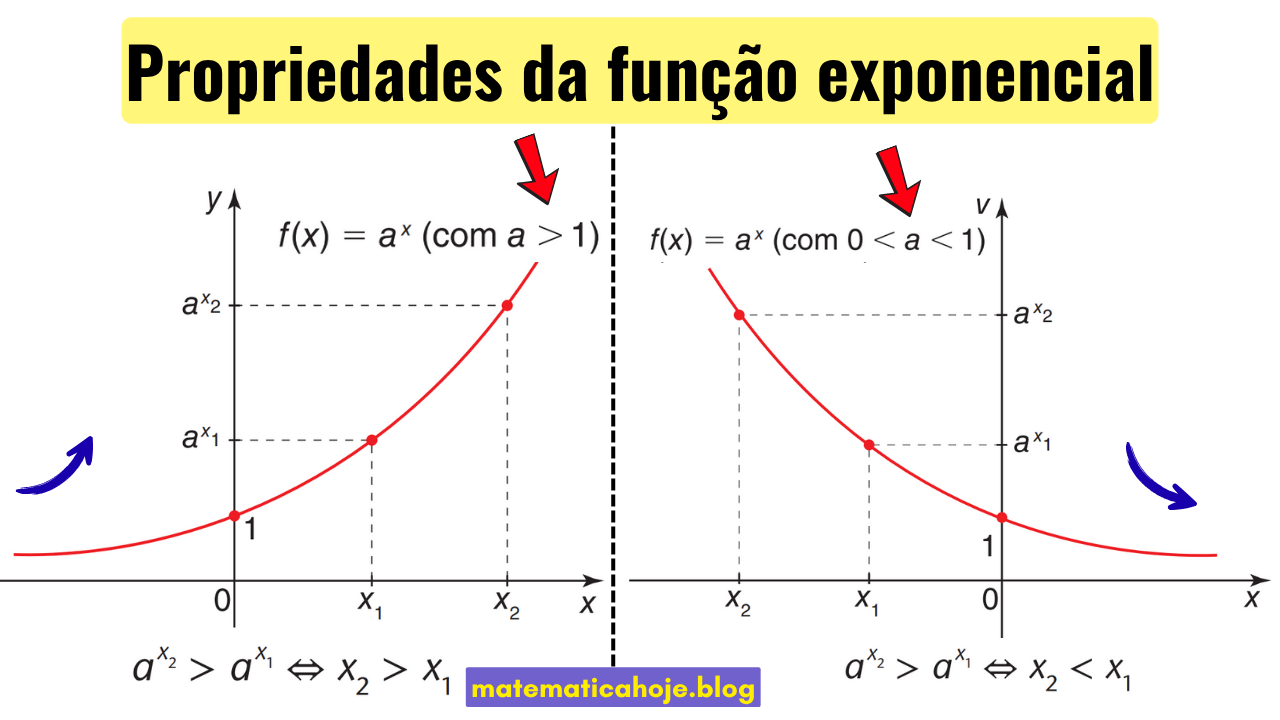
A função exponencial é definida por:
\[ f(x) = a^x \quad (a > 0, \; a \neq 1) \]
O comportamento depende do valor da base:
- Se \(a > 1\): a função é crescente.
- Se \(0 < a < 1\): a função é decrescente.
1) Principais propriedades
- Domínio: todos os números reais \(\mathbb{R}\).
- Imagem: valores positivos \((0,+\infty)\).
- Ponto comum: toda função exponencial passa por \(f(0)=1\).
- Assíntota: eixo \(x\) como reta assintótica horizontal.
- Monotonicidade: crescente para \(a>1\), decrescente para \(0
2) Comparação entre bases
Se \(a>1\): \(x_2 > x_1 \Rightarrow a^{x_2} > a^{x_1}\).
Se \(0
3) Exemplos resolvidos
Exemplo: Resolva \(3^x = 81\).
Como \(81 = 3^4\), temos \(3^x = 3^4 \Rightarrow x=4\).
Resposta: \(x=4\).
📘 Aprenda todas as fórmulas essenciais de matemática!
Baixe grátis o eBook Fórmulas Matemática
Baixe grátis o eBook Fórmulas Matemática
4) Exercícios de múltipla escolha
(1) Resolva a equação \(2^x = 16\).
- A) 2
- B) 3
- C) 4
- D) 5
\(16 = 2^4 \Rightarrow x=4\).
Resposta correta: C.
(2) Qual é o valor de \(f(-2)\) para \(f(x)=5^x\)?
- A) 1/25
- B) 25
- C) -25
- D) 5
\(f(-2)=5^{-2}=1/25\).
Resposta correta: A.
(3) A função \(f(x)=(1/2)^x\) é:
- A) Crescente
- B) Decrescente
- C) Constante
- D) Linear
Como \(0Resposta correta: B.













