Quadrilátero Inscrito na Circunferência
Um quadrilátero inscrito é aquele cujos quatro vértices pertencem a uma mesma circunferência. Essa configuração especial garante propriedades notáveis que facilitam a resolução de problemas de geometria.
Definição
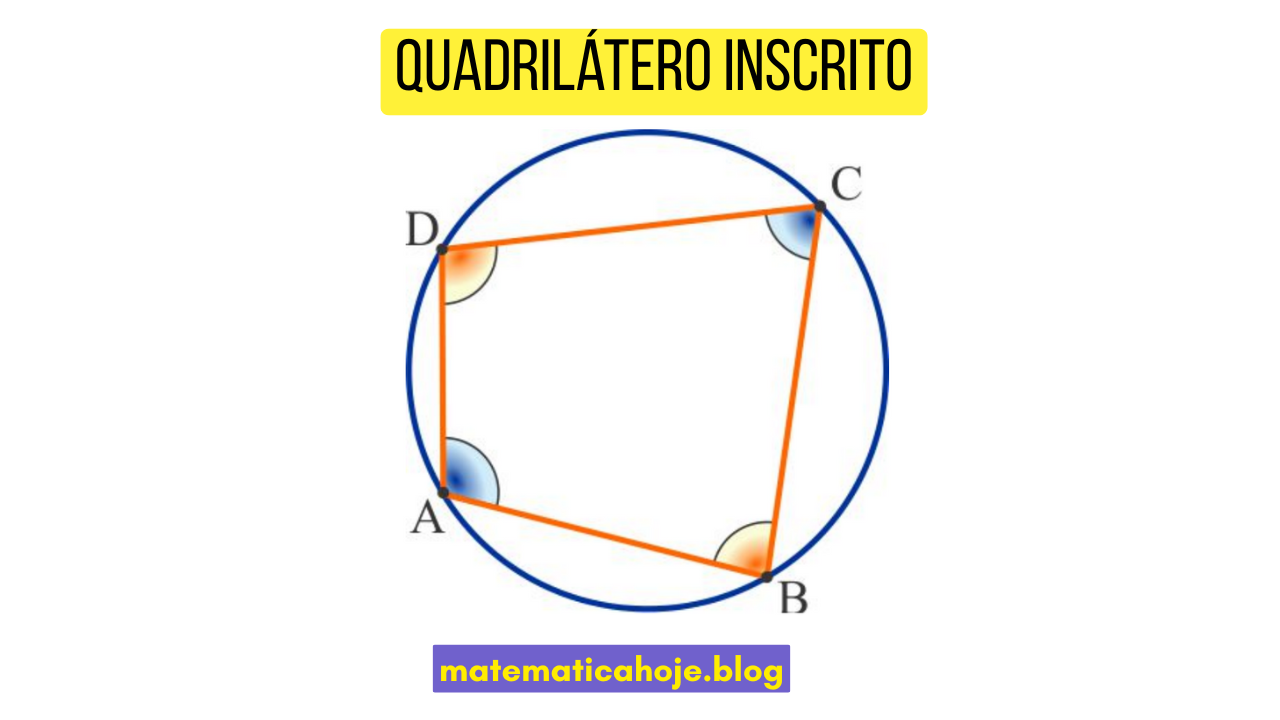
Seja um quadrilátero \(ABCD\). Ele será chamado de inscrito se existir uma circunferência que passa exatamente por seus quatro vértices.
Propriedade fundamental
Em todo quadrilátero inscrito, a soma dos ângulos opostos é igual a 180°:
\( \angle A + \angle C = 180^\circ \quad \text{e} \quad \angle B + \angle D = 180^\circ \)
Essa propriedade é consequência direta do ângulo inscrito e de sua relação com o arco correspondente.
Teorema de Pitot (caso especial)
Se o quadrilátero inscrito for tangencial (possui uma circunferência interna tangente a todos os lados), vale ainda:
\( AB + CD = BC + DA \)
Exemplo resolvido
Exemplo:
No quadrilátero inscrito \(ABCD\), sabemos que \(\angle A = 75^\circ\) e \(\angle C = 95^\circ\). Qual a medida do ângulo \(\angle B\)?
Solução:
Pela propriedade, \(\angle A + \angle C = 180^\circ\).
\(75^\circ + 95^\circ = 170^\circ\). Como deveria ser \(180^\circ\), temos um erro aparente: na verdade, o ângulo \(C\) precisa ser \(105^\circ\).
Assim, \(\angle A + \angle C = 75^\circ + 105^\circ = 180^\circ\).
Logo, \(\angle B + \angle D = 180^\circ\). Se \(\angle B = x\), então \(\angle D = 180^\circ – x\).
📘 Exercícios de múltipla escolha
1) Em um quadrilátero inscrito, \(\angle A = 70^\circ\) e \(\angle C = ?\)
- \(70^\circ\)
- \(90^\circ\)
- \(110^\circ\)
- \(120^\circ\)
Ver solução
\(\angle A + \angle C = 180^\circ \Rightarrow \angle C = 180^\circ – 70^\circ = 110^\circ\).
2) Se \(\angle B = 85^\circ\), então \(\angle D = ?\)
- \(85^\circ\)
- \(90^\circ\)
- \(95^\circ\)
- \(95^\circ\)
Ver solução
\(\angle B + \angle D = 180^\circ \Rightarrow \angle D = 180^\circ – 85^\circ = 95^\circ\).
Links úteis
📚 Continue estudando
O estudo dos quadriláteros inscritos é essencial para a geometria e cai bastante em provas de concursos e vestibulares.






















