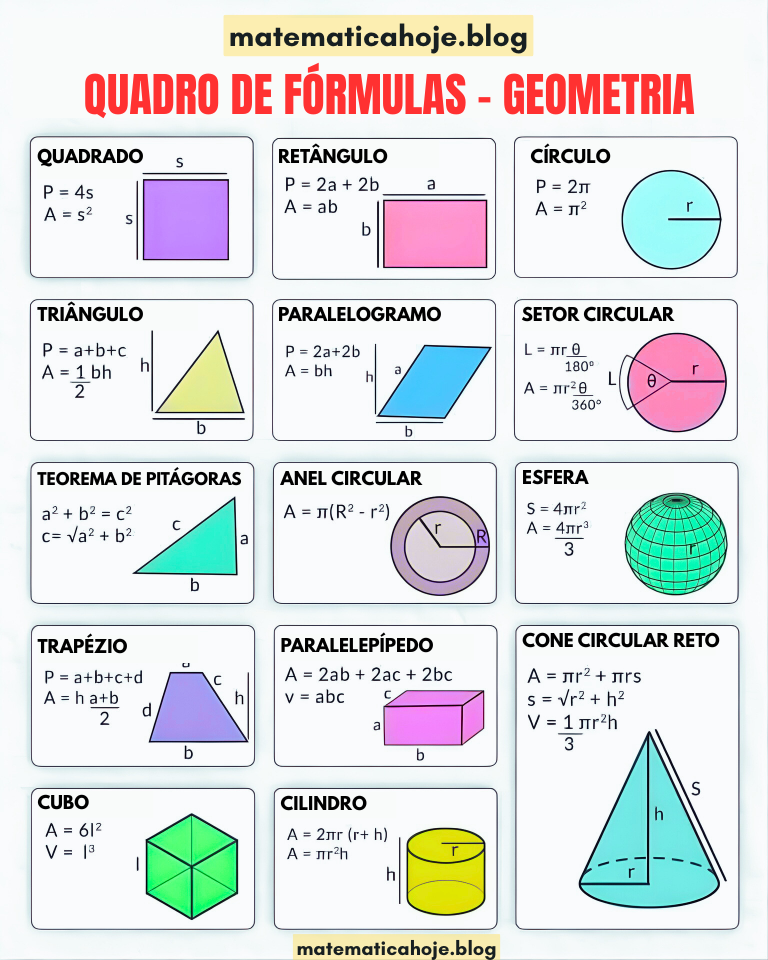
Quadro de Fórmulas – Geometria (Figuras Planas e Espaciais): Área, Perímetro, Volume e Exercícios Resolvidos
Guia completo e didático de Geometria Plana com fórmulas de quadrado, retângulo, triângulo, círculo, paralelogramo e trapézio. Inclui explicações passo a passo, três exercícios resolvidos por tema e links para conteúdos relacionados do blog.
| ENEM Matemática: guia de estudos |
| Banco de Questões de Matemática |
| Coleção com 10 eBooks de Matemática |
1) Quadrado — Área e Perímetro
Para um quadrado de lado $s$:
Exercícios Resolvidos (3)
Exercício 1 — lado 6 cm
Com $s=6$: $P=4\cdot6=24$ cm e $A=6^2=36\ \text{cm}^2$.
Exercício 2 — área conhecida
Se $A=144\ \text{cm}^2$, então $s=\sqrt{144}=12$ cm e $P=4\cdot12=48$ cm.
Exercício 3 — perímetro 40 cm
$P=4s=40 \Rightarrow s=10$ cm. Área: $A=10^2=100\ \text{cm}^2$.
2) Retângulo — Área e Perímetro
Para lados $a$ e $b$:
Exercícios Resolvidos (3)
Exercício 1 — $a=8$ cm, $b=3$ cm
$P=2(8)+2(3)=16+6=22$ cm. $A=8\cdot3=24\ \text{cm}^2$.
Exercício 2 — área 60 cm² e base 12 cm
$A=ab=60$ e $a=12 \Rightarrow b=60/12=5$ cm. $P=2(12)+2(5)=34$ cm.
Exercício 3 — perímetro 50 cm e $a=15$ cm
$2a+2b=50 \Rightarrow 2b=20 \Rightarrow b=10$ cm. $A=15\cdot10=150\ \text{cm}^2$.
3) Triângulo — Perímetro e Área
Com lados $a,b,c$ e base $b$ e altura $h$:
Exercícios Resolvidos (3)
Exercício 1 — $b=10$ cm e $h=6$ cm
$A=\frac{10\cdot6}{2}=30\ \text{cm}^2$.
Exercício 2 — lados 7, 9 e 12 cm
$P=7+9+12=28$ cm.
Exercício 3 — área 48 cm² e base 12 cm
$A=\frac{b h}{2}=48 \Rightarrow h=\frac{2\cdot48}{12}=8$ cm.
4) Círculo — Circunferência e Área
Para raio $r$:
Exercícios Resolvidos (3)
Exercício 1 — $r=7$ cm
$C=2\pi\cdot7=14\pi$ cm; $A=\pi\cdot7^2=49\pi\ \text{cm}^2$.
Exercício 2 — diâmetro 20 cm
Diâmetro $d=20 \Rightarrow r=10$. $C=20\pi$ cm; $A=100\pi\ \text{cm}^2$.
Exercício 3 — área $64\pi\ \text{cm}^2$
$\pi r^2=64\pi \Rightarrow r^2=64 \Rightarrow r=8$ cm. $C=16\pi$ cm.
Baixe agora: Mapas Mentais de Matemática
O material visual que acelera suas revisões e fixa as fórmulas deste artigo.
Acessar Mapas MentaisE não esqueça do E-book Fórmulas Matemática
Todas as fórmulas essenciais de Geometria, Álgebra, Aritmética e muito mais — prontas para impressão.
Baixar gratuitamente5) Paralelogramo — Área e Perímetro
Com base $b$, altura $h$ e lados $a$ e $b$:
Exercícios Resolvidos (3)
Exercício 1 — $b=12$ cm e $h=5$ cm; $a=9$ cm
$A=12\cdot5=60\ \text{cm}^2$; $P=2(9)+2(12)=18+24=42$ cm.
Exercício 2 — $A=96\ \text{cm}^2$ e $b=16$ cm
$h=A/b=96/16=6$ cm.
Exercício 3 — $P=58$ cm, $a=13$ cm e $b=?$
$2a+2b=58 \Rightarrow 26+2b=58 \Rightarrow 2b=32 \Rightarrow b=16$ cm.
6) Trapézio — Perímetro e Área
Com bases $a$ e $b$, lados não paralelos $c$ e $d$ e altura $h$:
Exercícios Resolvidos (3)
Exercício 1 — $a=12$ cm, $b=8$ cm, $h=5$ cm
$A=\dfrac{(12+8)\cdot5}{2}=\dfrac{20\cdot5}{2}=50\ \text{cm}^2$.
Exercício 2 — $a=10$ cm, $b=14$ cm, $c=7$ cm, $d=9$ cm
$P=10+14+7+9=40$ cm.
Exercício 3 — área 84 cm², $a=9$ cm, $b=15$ cm
$A=\dfrac{(a+b)h}{2}=84 \Rightarrow h=\dfrac{2\cdot84}{9+15}=\dfrac{168}{24}=7$ cm.
Continue estudando com o nosso Banco de Questões
Milhares de itens para treinar todas as fórmulas deste quadro.
Acessar Banco de QuestõesReforce com a coleção 10 eBooks de Matemática
Ver os 10 eBooks7) Setor Circular — Arco e Área
Para um círculo de raio $r$ e ângulo central $\theta$ (em graus):
Exercícios Resolvidos (3)
Exercício 1 — $r=6$ cm e $\theta=120^\circ$
Arco: $L=\dfrac{\pi\cdot6\cdot120}{180}= \dfrac{720\pi}{180}=4\pi$ cm.
Área: $A=\dfrac{\pi\cdot6^2\cdot120}{360}=\dfrac{36\pi\cdot120}{360}=12\pi\ \text{cm}^2$.
Exercício 2 — área do setor $25\pi\ \text{cm}^2$, $r=10$ cm. Determine $\theta$.
$A=\dfrac{\pi r^2\theta}{360}=25\pi \Rightarrow \dfrac{\pi\cdot100\cdot\theta}{360}=25\pi$.
Corta $\pi$: $\dfrac{100\theta}{360}=25 \Rightarrow 100\theta=9000 \Rightarrow \theta=90^\circ$.
Exercício 3 — comprimento do arco $15{,}7$ cm e $r=5$ cm. Encontre $\theta$ (graus).
Use $\pi\approx3{,}14$. $L=\dfrac{\pi r\theta}{180} \Rightarrow 15{,}7=\dfrac{3{,}14\cdot5\cdot\theta}{180}$.
$15{,}7=\dfrac{15{,}7\theta}{180} \Rightarrow \theta=180^\circ$.
Veja também: exercícios de círculo e revisão de Geometria Plana.
8) Anel Circular — Área
Anel formado por dois círculos concêntricos de raios $R$ (maior) e $r$ (menor):
Exercícios Resolvidos (3)
Exercício 1 — $R=10$ cm e $r=6$ cm
$A=\pi(10^2-6^2)=\pi(100-36)=64\pi\ \text{cm}^2$.
Exercício 2 — área $45\pi\ \text{cm}^2$ e $r=3$ cm. Encontre $R$.
$\pi(R^2-3^2)=45\pi \Rightarrow R^2-9=45 \Rightarrow R^2=54 \Rightarrow R=3\sqrt{6}$ cm.
Exercício 3 — larg. do anel $d=R-r$ é 2 cm e $r=7$ cm. Calcule a área.
$R=r+d=7+2=9$ cm. $A=\pi(9^2-7^2)=\pi(81-49)=32\pi\ \text{cm}^2$.
Dica visual — Mapas Mentais de Matemática
Resumo gráfico de círculos, setores e anéis para memorização rápida.
Acessar Mapas MentaisE-book Fórmulas Matemática (gratuito)
Leve as fórmulas de Geometria para impressão e revisão off-line.
Baixar agora9) Teorema de Pitágoras
Em um triângulo retângulo com catetos $a$ e $b$ e hipotenusa $c$:
Exercícios Resolvidos (3)
Exercício 1 — $a=6$ cm e $b=8$ cm
$c=\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10$ cm.
Exercício 2 — escada encostada: base 1,8 m e altura 2,4 m. Encontre o comprimento.
$c=\sqrt{1{,}8^2+2{,}4^2}=\sqrt{3{,}24+5{,}76}=\sqrt{9}=3$ m.
Exercício 3 — hipotenusa 13 cm e cateto 5 cm. Determine o outro cateto.
$a^2+b^2=13^2 \Rightarrow b^2=169-5^2=169-25=144 \Rightarrow b=12$ cm.
Aprofunde: triângulos retângulos e ENEM Matemática.
Pratique mais no Banco de Questões
Listas focadas em círculo, setor, anel e aplicações de Pitágoras.
Treinar agoraReforço completo com os 10 eBooks de Matemática
Ver coleção10) Esfera — Área e Volume
Para uma esfera de raio $r$:
Exercícios Resolvidos (3)
Exercício 1 — $r=3$ cm
$S = 4\pi\cdot3^2 = 36\pi$ cm²; $V = \dfrac{4}{3}\pi\cdot3^3 = 36\pi$ cm³.
Exercício 2 — volume $36\pi$ cm³, determine $r$.
$\dfrac{4}{3}\pi r^3 = 36\pi \Rightarrow r^3 = 27 \Rightarrow r=3$ cm.
Exercício 3 — raio 7 cm, calcule área e volume (use $\pi\approx3{,}14$).
$S = 4\pi\cdot49 = 196\pi \approx 615{,}4$ cm²;
$V = \dfrac{4}{3}\pi\cdot343 = \dfrac{1372}{3}\pi \approx 1436{,}8$ cm³.
11) Paralelepípedo — Área e Volume
Com dimensões $a$, $b$ e $c$:
Exercícios Resolvidos (3)
Exercício 1 — $a=5$ cm, $b=3$ cm, $c=2$ cm
$A=2(5\cdot3+5\cdot2+3\cdot2)=2(15+10+6)=2(31)=62$ cm²;
$V=5\cdot3\cdot2=30$ cm³.
Exercício 2 — volume 120 cm³ e $a=5$ cm, $b=4$ cm. Encontre $c$.
$V=abc=120 \Rightarrow c=120/(5\cdot4)=120/20=6$ cm.
Exercício 3 — área total 94 cm² e dimensões $a=4$ cm, $b=3$ cm. Encontre $c$.
$2(ab+ac+bc)=94 \Rightarrow ab+ac+bc=47$;
$12+4c+3c=47 \Rightarrow 7c=35 \Rightarrow c=5$ cm.
12) Cubo — Área e Volume
Para aresta $l$:
Exercícios Resolvidos (3)
Exercício 1 — $l=4$ cm
$A=6\cdot4^2=6\cdot16=96$ cm²; $V=4^3=64$ cm³.
Exercício 2 — volume 125 cm³, encontre $l$.
$l^3=125 \Rightarrow l=5$ cm; $A=6\cdot5^2=150$ cm².
Exercício 3 — área 216 cm², determine o volume.
$6l^2=216 \Rightarrow l^2=36 \Rightarrow l=6$ cm; $V=6^3=216$ cm³.
13) Cilindro — Área e Volume
Com raio $r$ e altura $h$:
Exercícios Resolvidos (3)
Exercício 1 — $r=3$ cm e $h=10$ cm
$A=2\pi\cdot3(3+10)=6\pi\cdot13=78\pi$ cm²; $V=\pi\cdot3^2\cdot10=90\pi$ cm³.
Exercício 2 — volume $150\pi$ cm³ e $r=5$ cm. Encontre $h$.
$\pi r^2h=150\pi \Rightarrow 25h=150 \Rightarrow h=6$ cm.
Exercício 3 — área lateral $2\pi rh=94,2$ cm² e $r=5$ cm. Encontre $h$.
$2\pi rh=94,2 \Rightarrow h=94,2/(2\pi\cdot5)=94,2/(31,4)=3$ cm.
14) Cone Circular Reto — Área e Volume
Com raio $r$, altura $h$ e geratriz $s$:
Exercícios Resolvidos (3)
Exercício 1 — $r=3$ cm e $h=4$ cm
$s=\sqrt{3^2+4^2}=5$ cm;
$A=\pi\cdot3^2+\pi\cdot3\cdot5=9\pi+15\pi=24\pi$ cm²;
$V=\dfrac{1}{3}\pi\cdot3^2\cdot4=12\pi$ cm³.
Exercício 2 — volume $48\pi$ cm³ e $r=6$ cm
$V=\dfrac{1}{3}\pi r^2h=48\pi \Rightarrow 12h=48 \Rightarrow h=4$ cm.
Exercício 3 — área total $96\pi$ cm² e $r=6$ cm. Determine $s$.
$\pi r^2+\pi r s=96\pi \Rightarrow 36+6s=96 \Rightarrow 6s=60 \Rightarrow s=10$ cm.
Mapas Mentais de Matemática
Visualize todas as fórmulas deste quadro de forma organizada e colorida.
Baixar Mapas MentaisE-book Fórmulas Matemática
PDF gratuito com todas as fórmulas de Geometria Plana e Espacial — ideal para concursos e ENEM.
Baixar E-bookContinue aprendendo com o Banco de Questões
Exercícios resolvidos e questões de provas anteriores sobre todos esses sólidos geométricos.
Acessar Banco de QuestõesQuer reforçar todo o conteúdo?
Baixe a coleção completa com 10 eBooks de Matemática.
Ver Coleção Completa