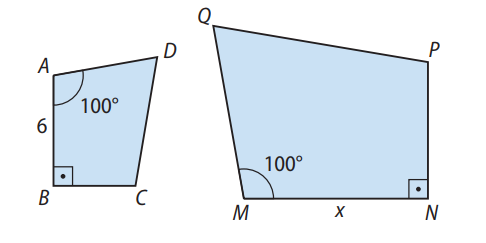
Os quadriláteros ABCD e MNPQ a seguir são semelhantes, e o lado AB do primeiro corresponde ao lado MN do segundo. Se a razão de semelhança do quadrilátero ABCD para o quadrilátero MNPQ é de \( \dfrac{3}{5} \), determine a medida do lado MN do quadrilátero MNPQ.
✅ Pratique mais: 6 Questões Resolvidas Sobre Figuras Semelhantes
A melhor forma de fixar conteúdo é praticando! Confira esta lista com 6 questões cuidadosamente resolvidas sobre figuras semelhantes, com passo a passo, explicações visuais e linguagem acessível.
👉 Acessar a lista de exercícios
