Questão 11 – Altura de um Trapézio Retângulo

Questão 11

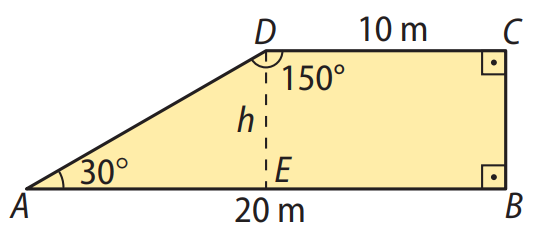
Enunciado: A soma dos comprimentos das bases de um trapézio retângulo vale 30 m. A base maior mede o dobro da menor. Calcule a altura do trapézio, sabendo que seu ângulo obtuso mede \(150^\circ\). Considere \(sen 30^\circ = 0,5.\)

Solução Passo a Passo:

1. Determinar as bases:

Seja \(x\) o valor da menor base. A base maior é \(2x\) e:

\(x + 2x = 30 \Rightarrow 3x = 30 \Rightarrow x = 10 \, \text{m}\)

Logo, as bases são 10 m e 20 m.

2. Determinar a altura usando o ângulo de \(30^\circ\):

No triângulo retângulo formado, temos:

\(tg 30^\circ = \frac{h}{10} \Rightarrow \frac{\sqrt{3}}{3} = \frac{h}{10} \Rightarrow h = \frac{10 \sqrt{3}}{3} \, \text{m}\)

Questão 11 - Trapézio

Resposta: A altura do trapézio é \(\frac{10 \sqrt{3}}{3} \, \text{m}\).

🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática

Relacionadas

Matemática para Concursos: Geometria Espacial – Banca VUNESP - Nível Superior

Matemática Banca IBFC: Geometria Espacial – Questão Comentada

Matemática Banca IBFC: Geometria Espacial – Questão Comentada

"Artigo escrito por"

Picture of Adriano Rocha

Adriano Rocha

Sou Adriano Rocha, professor de Matemática com mestrado e especialização em Resolução de Problemas, além de expertise em concursos públicos. Leciono no Colégio Estadual Mimoso do Oeste e utilizo metodologias inovadoras para aprimorar a compreensão matemática e a resolução de problemas. Produzo conteúdos como artigos para blogs, livros, eBooks e mapas mentais, além de desenvolver materiais didáticos e participar de eventos acadêmicos, sempre com o objetivo de contribuir para o ensino e aprendizagem da Matemática.

Nos ajude compartilhando esse post 😉

Facebook
WhatsApp
Twitter
Pinterest

👉🟢+ de 90 Mapas Mentais de Matemática

Veja também...

Questões

Conteúdo

Banca

Instagram Facebook Youtube
Rolar para cima