Questão 13
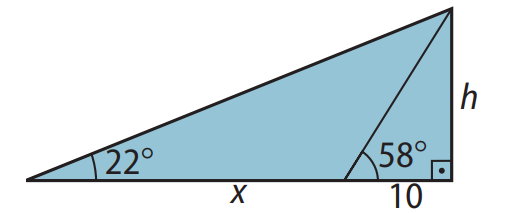
Enunciado: Uma pessoa, distante 10 m de um prédio, observa o topo dele sob um ângulo de \(58^\circ\). Ao afastar-se desse prédio, ainda observa o topo sob um ângulo de \(22^\circ\). Calcule a altura do prédio e a distância de afastamento entre os pontos de observação. Considere: \(tg 22^\circ = 0,4\) e \(tg 58^\circ = 1,6.\)
