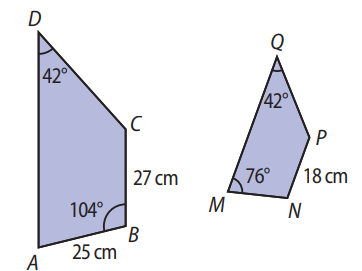
Os trapézios ABCD e MNPQ representados a seguir são semelhantes.
🔍 Análise dos trapézios semelhantes:
Sabemos que os trapézios ABCD e MNPQ são semelhantes. Isso significa que:
- Seus ângulos correspondentes são iguais;
- Seus lados correspondentes são proporcionais.
Ângulos correspondentes:
- \( \angle D = \angle Q = 42^\circ \)
- \( \angle B = \angle N = 104^\circ \)
Lados conhecidos:
- Base menor do trapézio maior: \( AB = 25\,\text{cm} \)
- Altura do trapézio maior: \( BC = 27\,\text{cm} \)
- Altura do trapézio menor: \( NP = 18\,\text{cm} \)
Vamos calcular a razão de semelhança:
\[ k = \frac{18}{27} = \frac{2}{3} \]
Com isso, podemos calcular a base menor do trapézio menor:
\[ MN = AB \cdot k = 25 \cdot \frac{2}{3} = \frac{50}{3} \approx 16{,}67\,\text{cm} \]
- Qual é a base menor do trapézio menor \( MN \), sabendo que a razão de semelhança é \( \frac{2}{3} \)?
- Sabendo que \( BC = 27\,\text{cm} \) e \( NP = 18\,\text{cm} \), qual é a razão de semelhança entre os trapézios?
✅ Resposta: As figuras são semelhantes, pois possuem ângulos congruentes e lados proporcionais. A razão de semelhança é \( \dfrac{2}{3} \) e a base menor do trapézio menor é aproximadamente 16,67 cm.
📚 Continue estudando com nossos materiais gratuitos:
✅ Pratique mais: 6 Questões Resolvidas Sobre Figuras Semelhantes
A melhor forma de fixar conteúdo é praticando! Confira esta lista com 6 questões cuidadosamente resolvidas sobre figuras semelhantes, com passo a passo, explicações visuais e linguagem acessível.
👉 Acessar a lista de exercícios












