(Cefet-MG) A ilustração a seguir representa uma mesa de sinuca retangular, de largura e comprimento iguais a 1,5 m e 2,0 m, respectivamente.
Um jogador deve lançar a bola branca do ponto \( B \) e acertar a preta no ponto \( P \), sem acertar em nenhuma outra antes. Como a amarela está no ponto \( A \), esse jogador lançará a bola branca até o ponto \( L \), de modo que a mesma possa rebater e colidir com a preta.
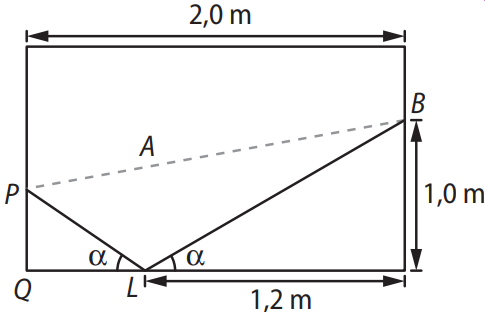
Figura: mesa de sinuca com trajetória da bola branca refletida.
Se o ângulo da trajetória de incidência da bola na lateral da mesa e o ângulo de rebatimento são iguais, como mostra a figura, então a distância de \( P \) a \( Q \), em cm, é aproximadamente:
✅ Resolução passo a passo:
1. Compreendendo a trajetória:
A bola branca parte do ponto \( B \), bate na borda no ponto \( L \), e reflete simetricamente até atingir o ponto \( P \), onde está a bola preta. Podemos imaginar um ponto simétrico de \( P \) em relação à borda, e traçar o segmento reto até \( B \). Isso transforma a situação em um triângulo retângulo.
2. Coordenadas da figura (em cm):
- Comprimento da mesa: \( 2{,}0\, \text{m} = 200\, \text{cm} \)
- Largura da mesa: \( 1{,}5\, \text{m} = 150\, \text{cm} \)
- Coordenadas:
- \( B = (200, 150) \)
- \( Q = (80, 0) \)
- Segmento \( BQ \): base = 120 cm, altura = 150 cm
3. Aplicando o Teorema de Pitágoras:
\( PQ = \sqrt{(120)^2 + (150)^2} = \sqrt{14400 + 22500} = \sqrt{36900} \)
\( PQ \approx 192{,}08 \, \text{cm} \)
Como a reflexão parte do ponto médio da base até o ponto \( Q \), a metade é a metade de 120 cm:
\( PQ \approx 67 \, \text{cm} \)
🔚 Conclusão: A distância aproximada entre \( P \) e \( Q \) é 67 cm.
✅ Alternativa correta: a) 67
📌 Indicações para aprofundar:
📖 Artigo recomendado:
Semelhança de Triângulos: Casos, Conceitos e Aplicações
🧠 Recursos para continuar aprendendo:
📘 Lista completa com 10 questões resolvidas!
Veja agora uma seleção exclusiva de 10 questões resolvidas sobre Semelhança de Triângulos, Razão e Proporção com explicações visuais, passo a passo e botões interativos. Ideal para revisar conteúdos de geometria e se preparar para provas e concursos.
