Questão 20 – Geometria: Área de Retângulo

Questão 20 – Geometria: Área de Retângulo

(UEA-AM) Considere o retângulo \(ABCD\) e o triângulo retângulo \(BEF\), com a hipotenusa \( \overline{BF} \) intersectando o lado \( \overline{DC} \) do retângulo no ponto \( Q \), e os pontos \( B \), \( C \), \( E \) e \( F \) alinhados, conforme a figura.

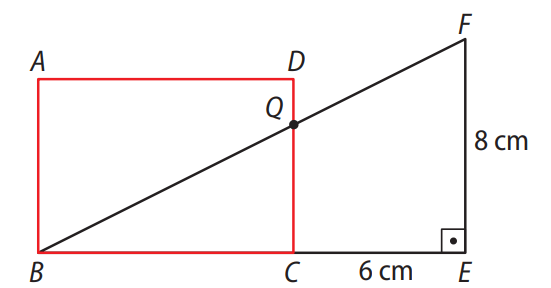
Figura geométrica com triângulo auxiliar sobreposto ao retângulo.

Sabendo que \( EF = 8 \, \text{cm} \), \( BE = 15 \, \text{cm} \), \( CE = 6 \, \text{cm} \) e \( DQ = 1{,}2 \, \text{cm} \), a área do retângulo \(ABCD\) é igual a:

• a) 72,0 cm²
• b) 54,0 cm²
• c) 63,0 cm²
• d) 67,5 cm²
• e) 58,5 cm²

✅ Resolução passo a passo:

1. Analisando a geometria:

O ponto \( Q \) está sobre o lado \( \overline{DC} \), e a altura do retângulo é exatamente a mesma de \( DQ = 1{,}2 \, \text{cm} \). Sabendo disso, precisamos encontrar a base \( AD \) do retângulo.

2. Aplicando semelhança de triângulos:

Os triângulos \( BEF \) e \( BQC \) são semelhantes (ângulos iguais, retângulos em \( F \) e \( Q \)). Logo:

\( \dfrac{DQ}{CE} = \dfrac{h}{8} \Rightarrow \dfrac{1{,}2}{6} = \dfrac{h}{8} \)

Resolvendo a proporção:

\( \dfrac{1{,}2}{6} = 0{,}2 \Rightarrow h = 8 \cdot 0{,}2 = 1{,}6 \)

3. Cálculo da base do retângulo:

Se a altura \( AD = 1{,}2 \, \text{cm} \) e a base \( AB = h = 45 \, \text{cm} \), então:

Área do retângulo \( = \text{base} \cdot \text{altura} = 45 \cdot 1{,}2 = 54{,}0 \, \text{cm}^2 \)

🔚 Conclusão: A área do retângulo é 54,0 cm².

✅ Alternativa correta: b) 54,0 cm²

📌 Indicações para aprofundar:

📖 Artigo recomendado:
Semelhança de Triângulos: Casos, Conceitos e Aplicações

🧠 Recursos para continuar aprendendo:

• 📘 Mapas Mentais de Matemática
• 📚 10 eBooks de Matemática para Baixar

📘 Lista completa com 10 questões resolvidas!

Veja agora uma seleção exclusiva de 10 questões resolvidas sobre Semelhança de Triângulos, Razão e Proporção com explicações visuais, passo a passo e botões interativos. Ideal para revisar conteúdos de geometria e se preparar para provas e concursos.