Questão 22: Variação Populacional em Relação à Temperatura
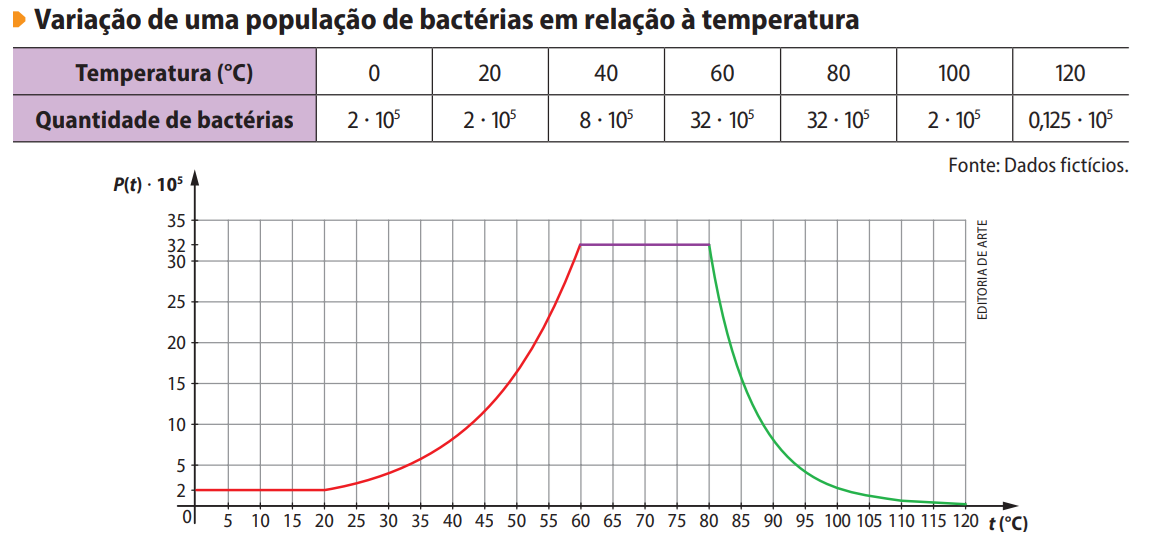
22. Uma amostra de bactérias foi estudada quanto ao seu crescimento e decréscimo populacional \( P \), em centenas de milhares, em relação ao aumento da temperatura \( t \), em °C. Nesse experimento, a temperatura foi aumentada progressivamente, partindo de 0 °C e terminando em 120 °C, em um período de 24 horas. Observe, a seguir, a tabela e o gráfico que descrevem a variação populacional dessa amostra.
-
a) Para quais intervalos de temperatura a população de bactérias estudada aumentou, diminuiu ou se manteve estável?
b) Se o aumento da população de bactérias é dado por \( f(t) = 2^{0{,}1(t – 10)} \) e a diminuição, por \( g(t) = 32 – 2^{0{,}2(t – 80)} \), calcule a quantidade aproximada de bactérias nessa amostra, quando a temperatura atingiu:
- 30 °C
- 50 °C
- 90 °C
- 110 °C
🔍 Ver solução passo a passo
🔎 Entendendo o enunciado:
Vamos analisar o gráfico e usar as expressões fornecidas para o aumento e a diminuição da população bacteriana, conforme a temperatura aumenta.
a) Intervalos de variação:
- Estável de 0 °C a 20 °C (população constante em \( 2 \cdot 10^5 \))
- Aumento de 20 °C a 60 °C (crescimento exponencial)
- Estável de 60 °C a 80 °C (população constante em \( 32 \cdot 10^5 \))
- Diminuição de 80 °C a 120 °C (decrescimento exponencial)
b) Cálculo das quantidades:
- Para 30 °C: \[ f(30) = 2^{0{,}1(30 – 10)} = 2^2 = 4 \Rightarrow 4 \cdot 10^5 = \boxed{400\,000\ bactérias} \]
- Para 50 °C: \[ f(50) = 2^{0{,}1(50 – 10)} = 2^4 = 16 \Rightarrow 16 \cdot 10^5 = \boxed{1\,600\,000\ bactérias} \]
- Para 90 °C: \[ g(90) = 32 – 2^{0{,}2(90 – 80)} = 32 – 2^2 = 32 – 4 = 28\]\[ \Rightarrow 28 \cdot 10^5 = \boxed{800\,000\ bactérias} \]
- Para 110 °C: \[ g(110) = 32 – 2^{0{,}2(110 – 80)} = \]\[ 32 – 2^6 = 32 – 64 = -32 \]\[\ (\text{não faz sentido físico, usamos valor da tabela: }\]\[ 0{,}5 \cdot 10^5 = \boxed{50\,000\ bactérias}) \]
✅ Resumo final:
- a) Aumentou de 20 °C a 60 °C; estável de 0–20 °C e 60–80 °C; diminuiu de 80–120 °C
- b)
30 °C: 400 000 bactérias
50 °C: 1 600 000 bactérias
90 °C: 800 000 bactérias
110 °C: 50 000 bactérias (aproximado da tabela)





























