📘 Questão 25 – Geometria – Teorema de Pitágoras
(Enem/MEC) Na figura apresentada abaixo, que representa o projeto de uma escada com 5 degraus da mesma altura, o comprimento total do corrimão é igual a:
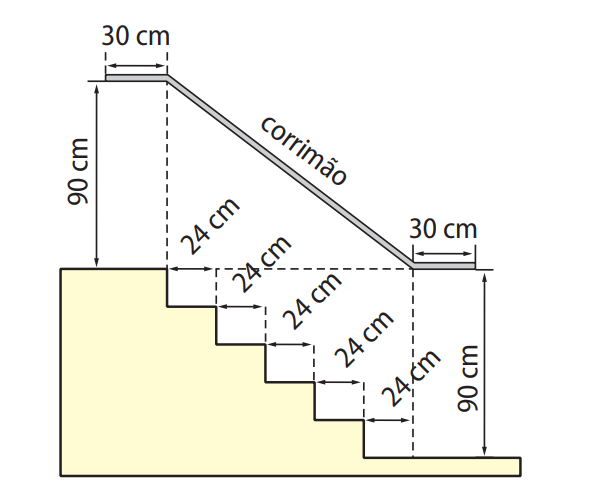
- a) 1,8 m
- b) 1,9 m
- c) 2,0 m
- d) 2,1 m
- e) 2,2 m
👀 Ver solução passo a passo
1. Clássico triângulo de Pitágoras:
Observamos que os catetos da escada formam proporção 3:4, o que indica o uso do triângulo pitagórico \( (3, 4, 5) \).
Somando os 5 degraus:
\[
24 + 24 + 24 + 24 + 24 = 120\,\text{cm}
\]
Altura total: \( 90\,\text{cm} \)
Aplicando o Teorema de Pitágoras: \[ 120^2 + 90^2 = C^2 \] \[ 14400 + 8100 = C^2 \] \[ C^2 = 22500 \Rightarrow C = \sqrt{22500} = 150\,\text{cm} \]
2. Abordagem alternativa (redução proporcional):
Podemos dividir os catetos por 30 para facilitar os cálculos:
\[
\frac{120}{30} = 4, \quad \frac{90}{30} = 3
\]
Aplicando o Teorema de Pitágoras:
\[
4^2 + 3^2 = C^2 \Rightarrow 16 + 9 = 25 \Rightarrow C = \sqrt{25} = 5
\]
Multiplicando novamente por 30 para voltar à proporção real:
\[
5 \times 30 = 150\,\text{cm}
\]
3. Corrimão completo:
Considerando as duas projeções horizontais de 30 cm em cada extremidade:
\[
150 + 30 + 30 = 210\,\text{cm} = 2{,}1\,\text{m}
\]
✅ Gabarito: Letra d) 2,1 m
🎯 Continue aprendendo com nossos materiais exclusivos:
