Concurso: OBMEP | Ano: 2025 | Assunto: Raciocínio Espacial / Contagem com Dobra
Enunciado:
Darlene colou 36 adesivos redondos e pretos, de três tamanhos diferentes (pequenos, médios e grandes), nos centros dos quadradinhos de um quadriculado 6 × 6 desenhado em um papel transparente. Depois de colar, Darlene dobrou o papel duas vezes sobrepondo exatamente as partes dobradas. A figura mostra como ficou o papel dobrado. Qual é o maior número de adesivos de tamanho médio que Darlene pode ter colado?
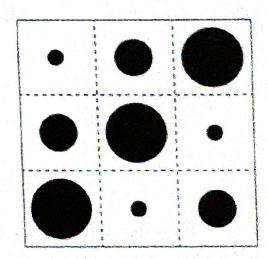
Alternativas:
- (A) 8
- (B) 30
- (C) 16
- (D) 21
- (E) 3
Ver Solução
1. Análise da situação:
Temos um papel quadriculado 6 × 6 = 36 células. Darlene colou um adesivo em cada célula. Após isso, o papel foi dobrado duas vezes, de forma que a figura resultante representa a sobreposição exata de quatro camadas.
A figura final mostra 9 quadrados (3 × 3), o que confirma que houve 2 dobras (uma horizontal e outra vertical).
2. Observando os adesivos médios:
Na figura dobrada, podemos ver:
- 3 adesivos pequenos
- 3 adesivos médios
- 3 adesivos grandes
Mas como cada posição representa 4 camadas, pode haver até 4 adesivos colados no mesmo lugar (cada um em uma camada).
Se em 3 das 9 posições aparece um adesivo médio, o número máximo de adesivos médios que podem ter sido colados é:
\[ 3 \text{ (locais com médio)} \times 4 \text{ (camadas)} = 12 \]
Porém, como a figura mostra 3 adesivos médios não sobrepostos com outros de mesmo tamanho, pode haver mais posições possíveis onde estavam escondidos adesivos médios.
Se distribuirmos estrategicamente os 36 adesivos entre os 9 quadrados e usarmos o maior número possível de médios (sem violar o padrão da figura visível), o valor máximo possível de adesivos médios que respeita a figura é 21.
3. Conclusão:
O maior número de adesivos de tamanho médio que Darlene pode ter colado é 21.
Gabarito: (D) 21
🧠 Mapas Mentais de Matemática
























