Questão 5
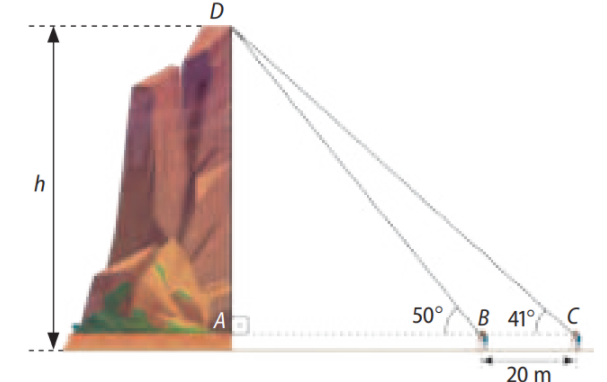
Enunciado: Retomando a situação da introdução do capítulo, determine a altura \(h\) do barranco, sabendo que o teodolito está a 1,6 m do solo, alinhado com a base do barranco. Considere:
\(tg 41^\circ = 0,87 \quad \text{e} \quad tg 50^\circ = 1,19\)
Solução Passo a Passo:
1. Triângulo ABD:
\(tg 50^\circ = \frac{h – 1,6}{AB} = 1,19 \Rightarrow h – 1,6 = 1,19 \cdot AB \tag{I}\)
2. Triângulo ADC:
\(tg 41^\circ = \frac{h – 1,6}{AB + 20} = 0,87 \Rightarrow h – 1,6 = 0,87 \cdot (AB + 20)\) \(\Rightarrow h – 1,6 = 0,87 \cdot AB + 17,4 \tag{II}\)
3. Sistema de Equações:
\(1,19 \cdot AB = 0,87 \cdot AB + 17,4\) \(0,32 \cdot AB = 17,4 \Rightarrow AB = \frac{17,4}{0,32} \approx 54,375\)
4. Altura do barranco:
\(h – 1,6 = 1,19 \cdot 54,375 \approx 64,71\) \(h = 64,71 + 1,6 = 66,31 \, \text{m}\)
Resposta: A altura aproximada do barranco é 66,31 m.
🔗 Confira nossos Mapas Mentais de Matemática
📚 Baixe nossos 10 eBooks de Matemática
Explore Mais Conteúdos de Trigonometria
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon












