Questão 5
(UFU-MG) Uma área delimitada pelas Ruas 1 e 2 e pelas Avenidas A e B tem a forma de um trapézio \( ADD’A’ \), com \( AD = 90 \, \text{m} \) e \( A’D’ = 135 \, \text{m} \), como mostra o esquema da figura abaixo:
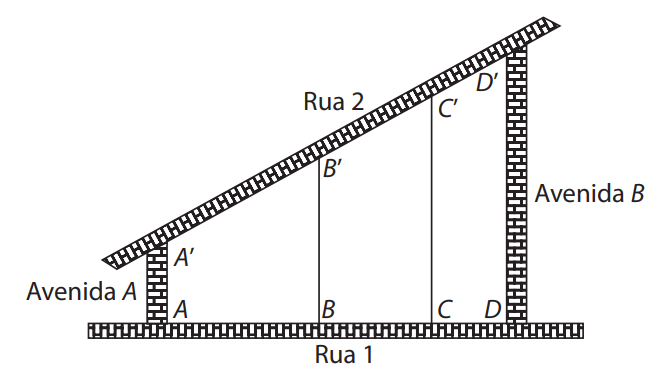
Essa área foi dividida em terrenos \( ABB’A’ \), \( BCC’B’ \) e \( CDD’C’ \), todos na forma trapezoidal, com bases paralelas às avenidas, tais que:
- \( AB = 40 \, \text{m} \)
- \( BC = 30 \, \text{m} \)
- \( CD = 20 \, \text{m} \)
De acordo com essas informações, a diferença, em metros, \( A’B’ – C’D’ \) é igual a:
- a) 20
- b) 30
- c) 15
- d) 45
Solução Passo a Passo:
O enunciado nos informa que os triângulos e trapézios são semelhantes, então podemos aplicar o Teorema de Tales para obter os valores de \( A’B’ \) e \( C’D’ \).
Sabemos que:
\[ \frac{AD}{A’D’} = \frac{AB}{A’B’} \Rightarrow \frac{90}{135} = \frac{40}{A’B’} \]
Multiplicando cruzado:
\[ 90 \cdot A’B’ = 135 \cdot 40 \] \[ A’B’ = \frac{135 \cdot 40}{90} = \frac{5400}{90} = 60 \]
Agora aplicamos o mesmo raciocínio para \( C’D’ \):
\[ \frac{AD}{A’D’} = \frac{CD}{C’D’} \Rightarrow \frac{90}{135} = \frac{20}{C’D’} \] \[ C’D’ = \frac{135 \cdot 20}{90} = \frac{2700}{90} = 30 \]
Portanto:
\[ A’B’ – C’D’ = 60 – 30 = \boxed{30 \, \text{m}} \]
Resposta correta: letra b.
📌 Aproveite também:
📚 Continue aprendendo!
✅ Confira a lista completa com 11 questões resolvidas de Matemática com gráficos e solução visual passo a passo:
👉 Acesse a lista completa de exercícios
📐 Aprofunde-se no conteúdo com o artigo completo sobre Relações Métricas no Triângulo Retângulo:
🔍 Leia o artigo completo agora
📚 Coleção de Livros Indispensáveis
Volume 3: Trigonometria
Domine a trigonometria com explicações claras, exemplos práticos e conteúdo completo para estudo.
🔗 Acesse na AmazonVolume 9: Geometria Plana
Estude os conceitos de geometria plana com uma abordagem didática e repleta de exemplos.
🔗 Acesse na AmazonVolume 10: Geometria Espacial
Aprofunde-se nos estudos da geometria espacial com conteúdos explicativos e exercícios práticos.
🔗 Acesse na Amazon












