Questão 9
(UFRGS-RS) Considere o retângulo \(ABCD\) de lados \( AB = 4 \) e \( AD = 2 \), e o ponto médio \( M \) de \( AB \).
Traçando a reta mediatriz do lado \( AB \), determina-se o segmento \( MN \), com \( N \) na interseção da mediatriz com \( DC \).
Considere um ponto \( P \) construído sobre o segmento \( MN \), e os segmentos \( PD \) e \( PC \), como mostra a figura abaixo.
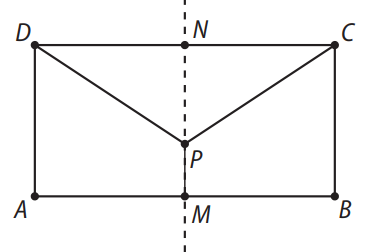
Tomando \( x \) como a medida do segmento \( PN \), considere \( S(x) \) a função que expressa a soma das medidas dos segmentos \( PM \), \( PD \) e \( PC \) em função de \( x \).
Para \( 0 \leq x \leq 2 \), \( S(x) \) é:
- a) \( x + 2\sqrt{x^2 + 4} \)
- b) \( (2 – x) + 2(x^2 + 4) \)
- c) \( (2 – x) + \sqrt{x^2 + 4} \)
- d) \( x + \sqrt{x^2 + 4} \)
- e) \( (2 – x) + 2\sqrt{x^2 + 4} \)
📚 Continue aprendendo!
✅ Confira a lista completa com 11 questões resolvidas de Matemática com gráficos e solução visual passo a passo:
👉 Acesse a lista completa de exercícios
📐 Aprofunde-se no conteúdo com o artigo completo sobre Relações Métricas no Triângulo Retângulo:
🔍 Leia o artigo completo agora
