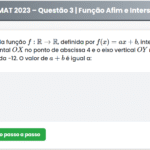
Considere as seguintes afirmações:
I – O conjunto \(A\) possui 120 elementos.
II – O conjunto \(A \cup B\) possui 216 elementos.
III- O conjunto \(A \cap B\) possui 24 elementos.
(A) II, apenas.
(B) III, apenas.
(C) I e II, apenas.
(D) I e III, apenas.
(E) I, II e III.
Solução Passo a Passo
1º Passo: Determinar os elementos de \(A\): Divisíveis por 8 em \(X\) são \(40, 48, \dots, 992\). Isto é \(5\cdot8, 6\cdot8, \dots, 124\cdot8\), totalizando 120 elementos.
2º Passo: Determinar os elementos de \(B\): Divisíveis por 10 em \(X\) são \(40, 50, \dots, 990\), ou seja \(4\cdot10, 5\cdot10, \dots, 99\cdot10\), totalizando 96 elementos.
3º Passo: Interseção \(A \cap B\): São os múltiplos de 40 em \(X\): \(40, 80, 120, \dots, 960\) → 24 elementos.
4º Passo: União \(A \cup B\): \[ |A \cup B| = |A| + |B| – |A \cap B| = 120 + 96 – 24 = 192 \]
5º Passo: Verificando as afirmações:
- I – Verdadeira
- II – Falsa (união tem 192, não 216)
- III – Verdadeira
Resposta: Alternativa D.
📚 Coleção: A Matemática do Ensino Médio
A Matemática do Ensino Médio – Volume 1
👉 Comprar Agora
A Matemática do Ensino Médio – Volume 2
👉 Comprar Agora
A Matemática do Ensino Médio – Volume 3
👉 Comprar Agora
A Matemática do Ensino Médio – Volume 4
👉 Comprar Agora
"Artigo escrito por"
