RAZÃO DE SEMELHANÇA – Geometria Espacial
Escala Linear \(k\), Áreas \(k^2\) e Volumes \(k^3\) (com exemplos e exercícios)
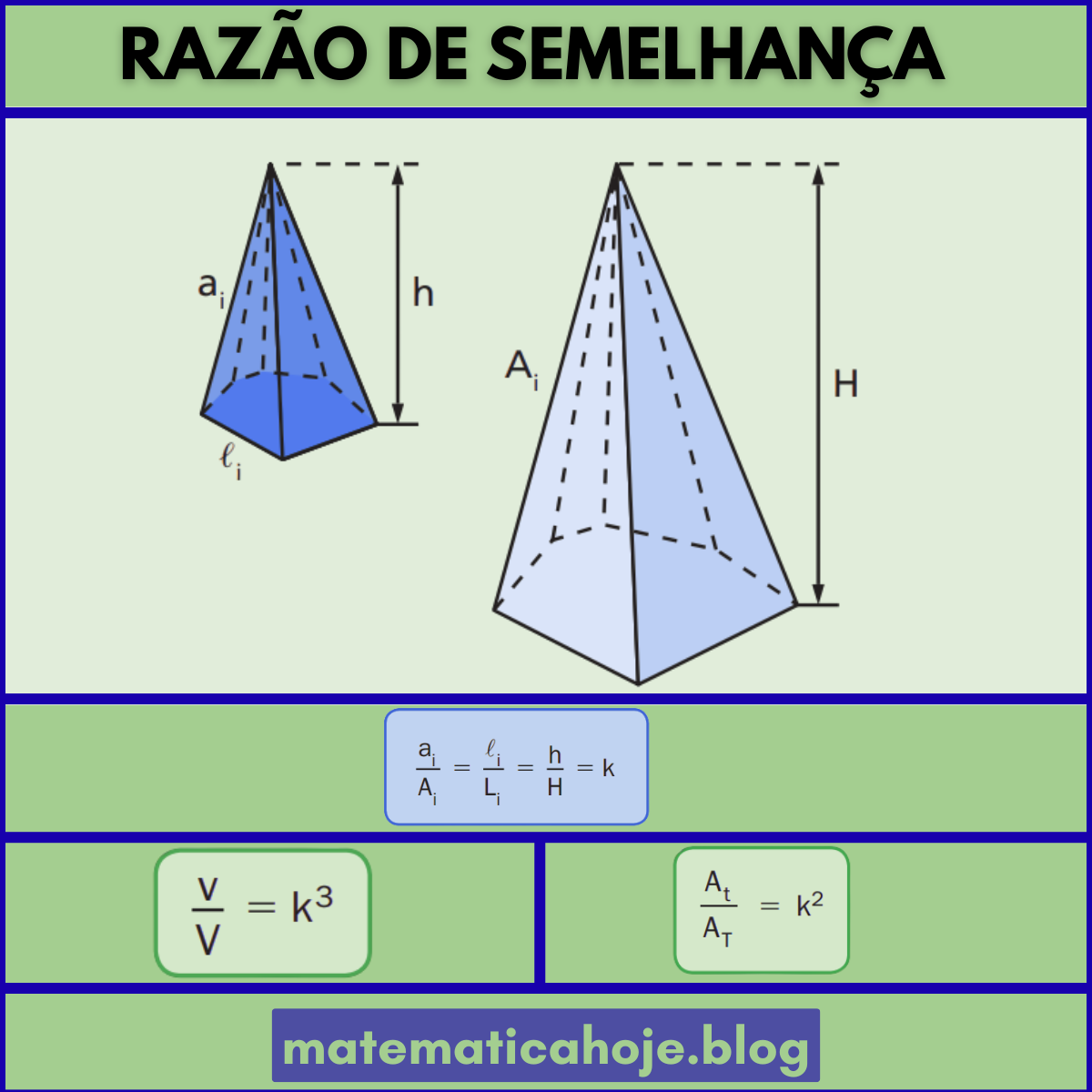
Quando dois sólidos são semelhantes?
Dois sólidos (pirâmides, prismas, cilindros, cones, esferas etc.) são semelhantes quando possuem a mesma forma, ou seja, ângulos correspondentes iguais e todas as dimensões lineares proporcionais. Se a razão entre quaisquer comprimentos correspondentes do pequeno para o grande é \(k\) (escala), então:
🧠 Veja os mapas
🎯 Guia completo
📘 Resolva exercícios
📚 Coleção completa
📘 Escalas de Semelhança
Lembrete: se o sólido maior tem dimensões multiplicadas por \(t\), então \(k=\dfrac{1}{t}\) do pequeno para o grande.
Exemplo 1 (cubo → escala direta)
Um cubo pequeno tem aresta \(2\,\text{cm}\) e outro cubo maior tem aresta \(5\,\text{cm}\). Encontre a razão de volumes \(V_p/V_g\).
📗 eBook de Fórmulas Matemáticas
Tenha todas as fórmulas (Álgebra, Geometria Espacial, Trigonometria…) num PDF enxuto para revisar antes das provas.
📥 Baixar AgoraExemplos Adicionais
Exemplo 2 (cones semelhantes). Dois cones semelhantes têm raios \(r_p=3\) e \(r_g=9\). Se a área lateral do grande é \(A_\ell^{(g)}=162\pi\), determine \(A_\ell^{(p)}\).
Exemplo 3 (cilindros – descobrindo a escala). O volume do cilindro A é \(V_A=500\pi\) e o do cilindro B (semelhante) é \(V_B=135\pi\). Qual é \(k=\dfrac{\text{A}}{\text{B}}\)?
Se preferir aproximação: \(\sqrt[3]{100}\approx 4{,}642\Rightarrow k\approx 1{,}547.\)
Exercícios de Múltipla Escolha
1. (Volume) Duas pirâmides regulares semelhantes têm alturas \(6\) cm e \(15\) cm. A razão \( \dfrac{V_{6}}{V_{15}} \) é:
👀 Ver solução passo a passo
Gabarito: C.
2. (Área) Dois prismas semelhantes têm razão linear \(k=\dfrac{3}{4}\) (pequeno para grande). Se \(A_{\text{total}}\) do grande é \(256\) cm², então o do pequeno é:
👀 Ver solução passo a passo
Gabarito: B.
3. (Descobrindo \(k\)) Dois cones semelhantes têm áreas totais \(A_{1}=200\pi\) e \(A_{2}=800\pi\). Qual é \(k=\dfrac{\text{cone 1}}{\text{cone 2}}\)?
👀 Ver solução passo a passo
Gabarito: A.
Conclusão
Em semelhança de sólidos, pense sempre: linear → \(k\), área → \(k^{2}\), volume → \(k^{3}\). Essa tríade resolve rapidamente questões do ENEM e concursos. Continue praticando com:













